(12th CLASS-12012)
MATHEMATICS, GROUP FIRST
OBJECTIVE
TIME: 30 MINS
MARKS: 20
NOTE: You have four choices for each objective type question as A , B C and D . The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Coning or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. Write the letter A, B, C or Dim the column (Write correct option) against each question. If there is a contradiction in the bubble and hand written answer, bubble option will be considered correct
QUESTION NO 1
SECTION-I
QUESTION NO. 2 Attempt any eight (8) short question
- Express the volum V of a ube as a function of the Area A of its Base.
- Evaluate
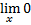
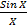
- Let y = 1/x3 , find sy
- If y = (ax + b)n then find sy
- Write the Quotient Rule for derivative of a function
- Find
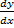 if xy + y2 = 2
if xy + y2 = 2
- Differentiate (Sin 2 θ – Cos 3θ )2 w.r.t θ
- Find f’(x) if f(x) =
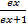
- Find y2 if y = In
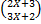
- Write Maclaun for a function f(x)
- Determine the interval in which f is increasing f(x) = Sinx
- Find dimension of a Rectangle of largest area having perimeter 120cm.
QUESTION NO. 3 Attempt any eight (8) short questions
- Using differentiate find
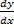 in xy- In x = c
in xy- In x = c
- Find
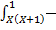 dx
dx
- Evaluate
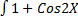 dx
dx
- Evaluate
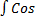 x (
x ( 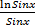 ) dx
) dx
- Evaluate
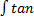 -1 x dx
-1 x dx
- Evaluate
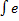 x (Cos x + Sin x) dx
x (Cos x + Sin x) dx
- Evaluate
 dx
dx
- Evaluate
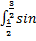 -1 x dx
-1 x dx
- Find area bound by curve y = x3+ 3x2 and x- axis
- Solve differentiate equation
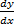 = - y
= - y
- Find objective function and optimal solution
- Graph the inequality x + 2y < 6
QUESTION NO. 4 Attempt any Nine (9) short questions.
- The point C (-5,3) is the center of a circle and p(7,-2) lies on the circle.
What is the radius of the circle?
- The XY – coordinates of (-5,3) are roted about the origin through angle
Θ = 300
- Find an equation of yhe line with x- intercept – 9 and slope – 4
- Write the linear equation ax+ by + c = 0 in the matrix form
- Find the center and radius of the circle 5x2+ 5y2+ 24x + 36y + 10 =0
- Write down equation of the tangent to the circle x2+ y2 = 25 at (5 cosθ,5 sinθ)
- Find the co-ordinates of the points of intersection of the line
2x + y = 5 and the circle x2 + y2 + 2x = 0
- Prove that the point (at2, 2at) lies on the parabola y2 = 4ax
- Find the vertices and center of ellipse x2 + 4y2 = 16
- Define hyperbola
- Find a and b so that the vector 3i – j + 4k and ai + bj – 2k are parallel
- Find the projection of a along b when a = 3i + j-k; b = -2i – j+ k
- Prove that a x (b+ c) + bx (c+a) + cx (a+b)=0
Note: Attempt any three questions form this section
5.(a) Find the 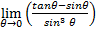
(b) If y =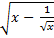 , show that 2x
, show that 2x 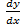 + y = 2
+ y = 2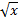
6.(a) Show that 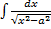 = in / x+
= in / x+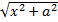 / + c
/ + c
(b) Derive the equation of straight line in two intercept from 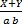 = 1
= 1
7.(a) Evaluate  dx
dx
(b) Graph the solution region the following system of linear ineqyalities and
Find the coner point
3 x + 2y > 6
X + 3y < 6
y> 0
8(a) write an equation of the circle that passes through the points A (5,10), B (6,9)
C (-2, 3)
(b) If a = 3i- j – 4k , b = -2i – 4i – 3k , c = i + 2j –k
Find a unit vector parallel to 3a- 2b + 4c
9.(a) Find an equations of the parabola with focus (-3,1) , Directrix x = 3
(b) A force F = 7i + 4j – 3k is applied at P ( 1, -2, 3) , Find its moment about
The point θ ( 2,1,1)