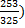FAISALABAD BOARD 2012
PAPER MATHEMATICS PART-I
Time: 30 Min.
(Objective Part)
Marks: 20
Note: Four Answers are given against each column A.11, C&D. Select the write answer and only separet answer sheet, fill the circle A, B, C or D with pen or marker in front of that question number.
- General solution set of the eq 1 + Cos x = 0
(a) {2n}; n𝜀 Z
(b) {n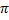 };n𝜀 Z
};n𝜀 Z
(c){ +2n
+2n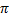 }= n𝜀 Z
}= n𝜀 Z
(d) { +2n
+2n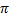 }; n𝜀 Z
}; n𝜀 Z
- (
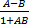 ) is equal to:
) is equal to:
(a) Tan-1 A + Tan-1 B
(b) Tan-1 A - Tan-1B
(c)Cot -1 A + Cot-1 B
(d) Cot-1 A - Cot-1B
- Value of circum radus R is:
(a) 
(b) 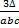
(c) 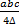
(d) 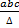
- The range of Cot x is:
(a) IR
(b)[ -1 ,1 ]
(c) IR – {x |x = n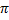 }
}
(d) IR-{x|x= (2n+1)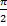 }
}
- If
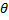 = 150°, then its reference angle is:
= 150°, then its reference angle is:
(a) 15°
(b) 30°
(c) 45°
(d) 60°
- Cot2
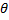 - cos ec2
- cos ec2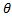 is equal to:
is equal to:
(a) -1
(b) 0
(c) 0
(d) 2
- The second term in the expansion of (1 +
 x)-1 is:
x)-1 is:
(a) 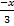
(b) 2x
(c) 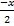
(d) 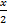
- The general term of the binomial expansion of (a+ x) n ,n𝜀N is:
(a) nCranxr
(b) nCrarxr
(c) nCr(ax)n-r
(d) nCran-rxr
- n2 > n+3 for all integral values of :
(a) n 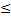 3
3
(b) n 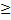 3
3
(c) n  2
2
(d) n  2
2
- The probability that an event E does not occur is:
(a) P(E)= 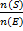
(b) P( )=
)= 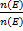
(c) P(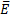 )= P(E) -1
)= P(E) -1
(d) P(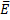 )= 1-P(E)
)= 1-P(E)
- The number of ways in which 5 person can be seated at a round table are:
(a) 2!
(b) 3!
(c) 4!
(d) 5!
- If "a" and "b" are two positive distinct real numbers, then:
(a) A> G
(b) A <G
(c) A = G
(d) A 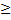 G
G
- The sum of n terms of an A.P. is n2. Then its common difference is:
(a) 4
(b) 2
(c) -2
(d) 1
- The partial fractions of
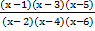 will be of the form:
will be of the form:
(a) 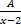 +
+ 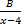 +
+ 
(b) 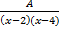 +
+ 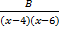
(c)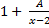 +
+ 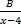 +
+ 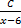
(d) 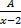 +
+ 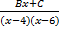
- The degree of constant polynomial is:
(a) 0
(b) 1
(c) 2
(d) 3
- If A = [
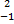 ] and B = [5 0] is equal to
] and B = [5 0] is equal to
(a) 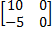
(b) [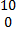 ]
]
(c) [0 0]
(d) [ ]
]
- A function
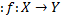 is called onto, if:
is called onto, if:
(a) Dom f = X
(b) Range f = Y
(c) Range f = X
(d) Domain f= range f
- If A = {0}, then P(A) (power set of set A) is:
(a) {0}
(b) {0,𝜙}
(c) {𝜙,(0)}
(d) {(0),( 𝜙)}
- Conjugate of - 2 + 3i is:
(a) -2-3i
(b) 2-3i
(c) 2 + 3i
(d) - 2 + 3i
- The set 10,11 is closed under:
(a) Addition
(b) Multiplication
(c) Subtraction
(d) Division
Time: 2:30 Hours
(Subjective Part)
Marks: 80
SECTION-1
2.Attempt any Eight Parts. 16s
- Simplify: (a + bi)3
- Define the difference of two sets.
- Show that the statement P
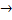 (P
(P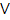 q) is a tautology.
q) is a tautology.
- Find the inverse of the relation {(x,y)|Y2 = 4ax,x
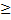 0}.
0}.
- Show that the set of natural numbers w.r.t. addition is not group.
- What is the transpose of a matrix?
- Without expansion show that
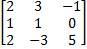 = 0
= 0
- If the matrices A and B are symmetric and AB = BA, show that AB is symmetric.
- Define radical equation with example.
- Evaluate: (1 +
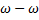 2)8
2)8
- Discuss the nature of the root of the equation x2 + 2x +3 =0.
- 3.Attempt any Eight Parts. 16
- Resolve into partial fractions:
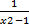
- Resolve into partial fractions:
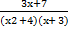
- Which term of A.P. -2, 4, 10,….. is 148 ?
- Find the sum of infinite geometric series:
 +
+ +1+…..
+1+….. 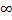
- Find the 9th, Term of harmonic sequence: -
 , -
, -  ,-1…
,-1…
- Evaluate: 10P7
- Find the values of n & r, when rCr = 35,n Pr = 210.
- A coin is tossed four times. Find the probability to get two heads and two tails.
- A natural number is chosen out of first fifty natural numbers. What is the probability
that chosen number is multiple of 3 or 5?
- Prove by induction that formula is true for all positive integer 'n' 1+5+9+……
+(4n-3)=n(2n-1).
- Find the term involsing y3 its the expansion of (x -
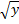 )11
)11
- If x is so small that its square and higher powers can be neglected then show that:
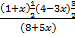
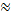 4(1-
4(1- 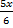 )
)
4. Attempt any Nine Parts. 18
- Convert the radian into the degree
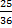
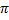 .
.
- Prove that Sin2
 + Sin2
+ Sin2  + Tan2
+ Tan2 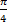 = 2
= 2
- Prove that Sin(180o +α).Sin(90° - α) = SinαCosα .
- Prove that
 = tan 56°
= tan 56°
- Express the product as sum or difference 2Cos5
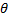 Sin3
Sin3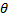
- Find the domain of tan
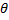 .
.
- Find the period of Sin3x.
- Solve the right triangle ABC in which
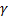 90o , α = 37°20' , α = 243.
90o , α = 37°20' , α = 243.
- Solve the triangle ABC in which β =125
 =53°, α= 47°.
=53°, α= 47°.
- Find the area of ABC if α = 200 , β =120
 = 150°.
= 150°.
- Find the solution of equation lie in (0,2
 ) Sinx =
) Sinx = 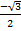
- Solve the trigonometric equation, tan2
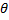 =
=
SECTION-II:Attempt any THREE questions. Each questions carries 10 marks.
5. (a) Let "G" be a group and a,b,c 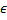 G. Then prove that
G. Then prove that
(i) ab = ac 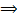 b = c (ii) ba = ca
b = c (ii) ba = ca 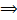 b = c holds in G.
b = c holds in G.
(b) Solve the matrix equa ion for matrix A when A
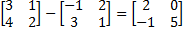
6. (a) Show that the roots of the equation
(a2 - bc)x2 + 2(b2 - ca)x + c2 - ab = 0 will be equal if either a3 +b3 +c3 = 3abc or b = 0.
(b) The nth term of the series is 3n2 + 2x +1 . Find the sum to 2n terms.
7. (a) Prove that n-1Cr + n-1Cr_1 = nCr.
(b) If A and B are square matrices and AB = Ba, then show by mathematical induction that ABn = Bn A for any positive integer n.
8. (a) Find the values of all trigonometric functions of - 
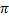 .
.
(b) Prove that Cos20°Cos40° Cos60° Cos80° =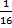 16 without use of calculator.
16 without use of calculator.
9.(a) Prove the law of sines of a triangle ABC. 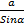 =
=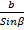 =
=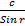
(b) Prove that (without using calculator),
Sin-5 ( )+ Sin-1 (
)+ Sin-1 (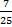 )= cos-1 (
)= cos-1 (