FAISALABAD BOARD 2012 
    PAPER MATHEMATICS
PART-II
Time: 30 Min. (Objective Part)
  Marks: 20

Note: Four Answers are given against each column A, B, C&D. Select the write answer and only separet answer sheet, fill the circle A, B, C or D with pen or marker in front of that question number.

• (k x i) x j equals to:
  (a) 1       
  (b)0       
  (c)k       
  (d)j
  
• Length of the vector –-2j+ 2k is:
  (a)3       
  (b)6       
  (c)4       
  (d)5
  
• Length of the major and minor axis of the ellipse are : 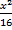+  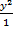=1
  (a)(4, 1)
  (b) (1, 4)              
  (c) (2, 1)              
  (d)(1, 2)
  
• Vertex of the parabola y2 = -4x + 4y is at:
  (a)(-1, 2)             
  (b)(1, 2)
  (c)(1, -2)              
  (d)(-1, -2)
  
  
• The radius of the circle x2 + y2 - 6x - 2y +1= 0 is:
  (a)3       
  (b)5       
  (c)2       
  (d)4
  
  
• A function which is to be maximized or minimized is called: 
  (a) Feasible function
  (b) Maximum function 
  (c) Minimum function   
  (d) Objective function
  
  
• Homogeneous equation of degree two ax2 +2hxy+by2 =0; where all a, b, h are not zero, repersents two real and coincident lines if:
  (a)h2 = ab           
  (b)h2 < ab
  (c)h2 > ab            
  (d) h2 = -ab
  
  
• Slope of the line passing through (4, 6) and (4, 8) is:
  (a)1                       
  (b)0       
  (c)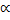      
  (d)4
  
• Solution of differential equation 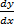  = 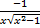 is:
  (a) y= Sec-1 x + c
  (b) y =Cosec-1 x + c
  (c) y = tan-1 x +c
  (d) y = Cot-1 x+c
  
  
• Area of region bounded by curve y = x2 and the x-axis from x = 0 to x = 2 is:
  (a)       
  (b)       
  (c)
  (d)4
  
  
  
•  dx is equal to
  (a)11     
  (b)21    
  (c)31     
  (d)41
  
• Value of 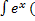 tan-1 x +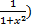dx is:
  (a)ex tan-1 x + c  
  (b) ex + tan-I x +c
  (C)ex + c
  (d)ex -tan-1 x +c
  
  
• Integral of 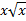 is :
  (a)  x5/2 + c
  (b)          x5/2 + c
  (c)  x5/2 + c
  (d)  x5/2 + x + c
  
  
• dx=? Wher m ≠ -1 is:
  (a)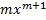 + c
  (b)(m+1)+ c
  (c) + c
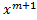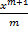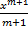  (d) + c
  
  
• If f(x) = tan x, then value of f(0) is:
  (a)1       
  (b)-1     
  (c)0       
  (d)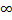
  
  
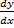• = x4 if y = : 
  (a) x5 
  (b) x5  
  (c)5x5
  (d)4x4
  
  
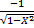•  is derivative of:
  (a)Cos-1 x            
  (b)Sin-1x
  (c)Tan-1x
  (d)Cot-1x
  
  
• Derivative of tan-1x is:
  (a)Cot-1x             
  (b)Sec-1 x
  (c)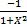 
  (d)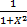
  
  
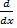• (-Cotx) is: 
  (a)-Cot x            
  (b) Co sec2 x
  (c)- Co sec2 x     
  (d)Cos x
  
•  =?
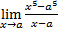  (a)5a4  
  (b)4a5
  (c)0       
  (d)Undefined

Time: 2:30 Hours 
 (Subjective Part)   
  Marks: 80

2.  Attempt any Eight Parts.      16

• Without finding the inverse, state the domain and range of f-1 
  if (x) = (x-5)2;x ≥ 5.
  
• Evaluate  .            
  
• Find the derivative f(x) =x3/2 w.r.t. 'x' by definition.
  
• If y=(3t + 2)-2 find by.
  
• Differentiate 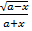w.r.t.' x'. 
  
• Differentiate 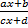 w.r.t.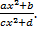           
  
• Differentiate Sin x w.r.t. Cot x.
  
• Find 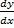 if y = 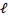n(x2 + 2x).
  
• Find 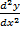 if x = at2,ybt4            
  
• Prove that: ex=1+ x + + ---------.  
  
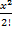• Determine the intervals in which f(x)= x2 +3x+2 ; xє( -4,1).
  
• Find the extreme value for the function f (x)= 3x2.
  

3.  Attempt any Eight Parts.                                                                                                         16

• Find σy and dy if y = 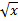 when x changes from 4 to 4.41.
  
• Evaluate 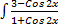dx.
  
• Evaluate
  
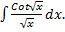
• Evaluate 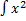. aax  dx .
  
• Evaluate 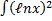dx.
  
• Evaluate  
  
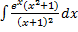
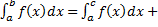
• Prove that  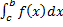 where a< c < b.
  
• Evaluate
  
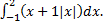
• Find area bonded by Cos function from x = 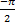to x =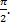             
  
• Solve  =.
  
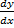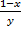• Define convex region.
  
• Indicate the solution region of x + y ≥ 5.
  

4. Attempt any Nine Parts.                                                                                                                          18

• Show that the points A (3, 1) , B (-2, -3) and C (2, 2) are vertices of an isosceles triangle.
  
• The x , y coordinate axes are rotated about origin through the angle 0, the new axes are OX, OY. Find X,Y coordinates of point P with given x,y coordinate p(5, 3)0 = 45°.
  
• Find equation of line bisecting first and 3rd. Quadrant.
  
• Detemine the value of P such that the lines 2x - 3y -1 = 0 and 3x - 5 = 0 and 3x + py + 8 = 0 meet at a point.
  
• Find equation of a circle whose centre is (h,k) and radius r.
  
• Find length of tangent drawn from (-5,4) to the circle 5x2 + 5y2 -10x +15y-131 =0
  
• Define the term diameter and chord of a circle.
  
• Write equation of a parabola when focus (-3,1) and directrix x = 3 are given.
  
• Find foci and eccentricity of ellipse 25x2 + 9y2 = 225.
  
• Define hyperbola. Write its equation in standard form.
  
• Find constant a so that the vectors V =I - 2j+3k and W = ai +6j- 9k are parallel.
  
• Define dot product of two vectors.
  
• Prove that the vectors i- 2j+ 3k ,-2i+3j-4k and i - 3j+ 5k are coplanar.
  

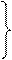
5. (a) Discuss the continuity of f(x) at x = 2 if :
f(x)=  2x + 5  if  x ≤ 2
4x + 1  if x > 2         
(b) Find 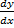 if x =  ,y =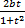
6. (a) Evaluate 
(b) Find the angles of the triangle whose vertices are A(-5,4), B(-2,-1), C(7,-5).
7. (a) Evaluate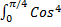t dt.
(b) Maximize f (x, y)=2x + 5y subject to constraints 2y-x ≤ 8,  x- y ≤ 4, x ≥ 0, y ≥ 0.
8. (a) Find an equation of a circle passing through the points A (5, 6), B (-3, 2) , C (3, -4).
(b) Prove (by vector method) that the line segment joining the mid points of the two sides of a triangle is parallel to the third side and half as long.
9. (a) Find the focus, vertex and directrix of the parabola y = 6x2 -1.
(b) Use vector method to prove
sin (α+ β)- sin αCosf β+ Cos α sin β