FAISALABAD BOARD 2012
PAPER STATISTICS
PART-II
Time: 20Minutes
Marks: 17

Note: Four Answers are given against each column A,B,C&D. Select the write answer and only separet answer sheet, fill the circle A,B,Cor D with pen or marker in front of that question number.

• (1-) is also called:

(a) Level of significance
(b) Confidence coefficient
(c) Size of the test
(d) Power of the test

• By decreasing , the length of confidence interval for µ is

(a) Increased
(b) Decreased
(c) No effect
(d) Difficult to tell

• Correlation coefficient is independent of:

(a) Units of measurements
(b) Change of origin
(c) Change of scale
(d) All of these

• If   = x + 10 and = y + 20 then "r" is:

(a) Zero
(b) 1
(c) -1
(d)

• If  = 10 and µ =12 , then sampling error: is:

(a) 2
(b) 0
(c) 10
(d) 12

• It is possible that two regression coefficients and correlation coefficient have:

(a) Different signs
(b) Same signs
(c) No sign
(d) Difficult to tell

• If x is a normal random variable with µ = 50 and σ = 7 , if y = x - 7 , then standard deviation of y is:

(a) Zero
(b) 7
(c) 14
(d) 49

• If x is N (100, 64), then second moment about mean is equal to:

(a) 100
(b) 64
(c) 36
(d) 8

• In sampling without replacement  is equal to:

(a)
(b)
(c)
(d)

• Increased demand of admission in the subject of computer in Pakistan is:

(a) Cyclical movement
(b) Secular trend
(c) Seasonal movement
(d) Random movement

• Keyboard, mouse, light pen and joy stick are the:

(a) Input devices
(b) Output devices
(c) Logical devices
(d) All of these

• Probability sampling and random sampling are:

(a) Same
(b) Different
(c) Opposite
(d) Difficult to tell

• The best fitting trend is one in which the sum of squares of residual is:

(a) Zero
(b) Maximum
(c) Least
(d) Residual

• The degree relationship between. two attributes is called:

(a) Regression
(b) Correlation
(c) Association
(d) Residual

• The normal distribution is:

(a) Positively skewed
(b)Negatively skewed
(c) Symmetrical
(d) All of these

• When the ranks are not correlated then Spearman's rank correlation coefficient is equal to:

(a) Zero
(b) -1
(c) +1
(d) -1 to +1

• Which is not null hypothesis?

(a) µ
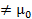
(b) µ=µ0
(c) µµ0
(d) µµ0

Time: 2:40 Hours
(Subjective Part)
Marks:68
SECTION-1

2. Write short answers of any Eight parts.     16

• Define normal distribution.
• If X is N (25, 25) find the value of maximum ordinate.
• If ZN (0, 1) verify that P (Z<2.5) is equal to P (Z>-2.5).
• Explain why odd order moments about mean equal to zero for normal distribution?
• Let XN (50, 10), find both quartiles of normal distribution.
• Define confidence interval.
• What is meant by estimation.
• Given N = 4, n = 2 & σ2 = 1.25 , if sampling is with replacement, then find E(s2) where S2 =
• Define text statistic.
• Explain with examples the difference between acceptance and rejection region.
• Differentiate between decimal number of system and binary number of system.
• Differentiate between RAM and ROM.

3. Write short answers of any Eight parts. 16

• What is population? 
• Why sampling is used?
• Differentiate with replacement sampling from without replacement sampling.
• If N = 50 , n = 25 and µp= 0.36 , find P and αp
• Explain sampling frame.
• Find α2 if α  = 2 and n = 4.
• Sketch scatter diagram indicating positive correlation.
• State two properties of regression equations.
• If byx = -0.2 and rxy = -0.80 obtain bxy.
• Show that the regression equations both y on x and x on y passes through the means x and y by writing the equations.
• What is the meaning of the statement that correlation coefficient is a pure number.
• Quote two examples one indicating positive correlation and the other negative correlation.

4. Write short answers of any Six parts.       12

• What is association?
• Define attributes.
• What are degree of freedom for ar x c contingency table?
• Define moving averages.
• Define analysis of time series.
• What is residual?
• Give the multiplicative model of time series.
• Give names of four components of time series.
• What are seasonal variations?

SECTION-II: Attempt any THREE questions. Each question carries 8 marks.

5.
(a) It is known that heights of young boys is normally distributed with mean 62" and S.D. 4". The maximum height required for joining Police Force is 64". Find the probability of boys who would be
(i) Accepted  
(ii) Rejected on account of their height. 04

(b) In a normal distribution µ = 47.6 , σ = 16.2. Find the probability
(i) two points such that 95% probability of falling between then
(ii) P90 04

6.(a) A population consists of four values i.e. 2, 4, 6 and 8. Out of which a sample of size two is drawn with replacement. Make the sampling distribution of means and thus show that:
(i) µ =µ         
(ii)       σ2 =. 04

(b) A sample of size two it drawn from a finite population having observation 1, 3, 6 and 9 without replacement. Making a sampling distribution of odd numbers, show that:
(i) 
(ii)     04
7.
(a) Find 90% confidence interval for the mean of a normal distribution of σ = 2 and if a sample of size n = 8 gave the values 9, 14, 10, 12, 7, 13, 11, 12. What would be the
confidence intervail if σ were unknown. 04
(b) The following data give paired yields of two varieties of wheat. Each pair was planted in a different locality. Test the hypothesis that the mean yields are equal.  04

8.
(a) From the following information.

n=20 x=25 y=35 ∑(x- x)²= 80
∑(y-y)²=170 ∑(x-x) (y-y) = -100

Show that the correlation coefficient is the geometric mean of regression coefficient.                                04
(b) Calculate ryz and rxy from the following data:       04

9.
(a) The result obtained by 300 students in Mathematics and  Statistics at Intermediate level are shown below:       04

Test at 5% level of significance, the performance in Mathematics
is independent from performance in Statistics.
(b) Find the trend line y = a+bx for the year 1996 - 2002 (both