Federal Board HSSC-I (2012)
MATHEMATICS
Time: 25 Minutes
Marks: 20
SECTION — A (Marks 20)
Q.1 Circle the correct option i.e. A/B/C/D. Each part carries one mark.
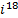 = ___________ .
= ___________ .
(A) 3
(B) 2
(C) 1
(D) -1
-
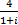 is :
is :
(A) 1 + i
(B) 1 - i
(C) 2(1 + i)
(D) 2(1 – i)
- (xc
 yc) = ___________ .
yc) = ___________ .
(A) x 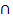 y
y
(B) x 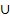 y
y
(C) (x 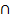 y)c
y)c
(D) None of these
- If
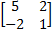 X =
X = 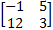 then X = _________
then X = _________
(A) 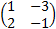
(B) 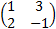
(C) 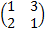
(D) 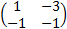
- (v) For what value of m, the roots of the equation (m+1)x2+2(m+3)x + m + 8=0 are equal?
(A) 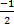
(B) 
(C) 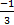
(D) None of these
- If
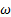 is the cube roots of unity, then a quadratic equation whose roots are 2
is the cube roots of unity, then a quadratic equation whose roots are 2 and 2
and 2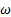 2 is :
2 is :
(A) x2 + 2x + 4 = 0
(B) x2 - 2x + 4 = 0
(C) x2 + x + 4 = 0
(D) x2 + 2x - 4 = 0
- If degree of P(x)=3 and degree of Q(x) = 4, then
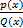 will be __________
will be __________
(A) Proper Rational FractionB.
(B) Improper Rational Fraction
(C) Polynomial
(D) None of these
- If a, b, c are in G.P and a > 0, b > 0, c > 0, then the reciprocals of a, b, c form
(A) A.P
(B) G.P
(C) HP
(D) None of these
- If
 ,
,  ,
,  are in A.P then the common difference is ________
are in A.P then the common difference is ________
(A) 
(B) 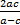
(C) 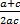
(D) 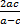
- A card is drawn from a pack of 52 cards at random. What is the probability that it is either a heart or a king?
(A) 
(B) 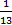
(C) 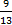
(D) 
- The middle terms in the expansion of
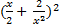 will be
will be
(A) 5th term
(B) 7th term
(C) 8th term
(D) 6th term
- Circular measure of the angle between the hands of a watch at a 4'0 clock is
(A)  radians
radians
(B) 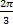 radians
radians
(C) 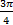 radians
radians
(D)  radians
radians
- If tan
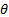 =
=  and 0 < θ <
and 0 < θ <  then
then 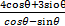 = __________
= __________
(A) 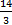
(B) 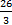
(C) 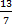
(D) None of these
- (xiv) The angles 90°
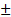 θ.180° ± θ,270°
θ.180° ± θ,270° 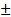 0,360° ± 0 are the______ angle.
0,360° ± 0 are the______ angle.
(A) Composite
(B) Half
(C) Quadrantal
(D) Allied
- The period of 3cos is
 is _______________
is _______________
(A) 5 π
(B) 2π
(C) 10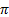
(D) 6π
- The in-radius r of a triangle is given by _______________
(A) 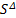
(B) 
(B) 
(D) None of these
- sin
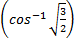 = ___________________
= ___________________
(A) 0
(B)
(C) 
(D) 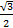
- If α and β are the roots of the equation x2 - (p - 1)x + c = 0 then (1 + α)(1 + β) = ___________
(A) 1 - c
(B) c - 2
(C) -c
(D) None of these
- Which term of 64, 60, 56, 52, ………. is zero?
(A) 16th
(B) 17th
(C) 14th
(D) 15th
- Multiplicative inverse of 1 - 2i is = __________
(A) 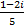
(B) 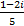
(C) 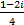
(D) None of these
MATHEMATICS HSSC-I
Time allowed: 2:35 Hours
Total Marks = 80
Note: Attempt any ten parts from Section 'B' and any five questions from Section 'C' on the separately provided answer book. Use supplementary answer sheet i.e.Sheet-B if required. Write your answers neatly and legibly.
SECTION - B (Marks 50)
Q.2 Attempt any TEN parts. All parts carry equal marks. (10 x 4 = 40)
- Simplify
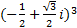
- Without expansion verify that
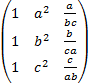 = 0
= 0
- Find the condition that
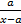 +
+ 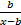 = 5 may have roots equal in magnitude but opposite in signs.
= 5 may have roots equal in magnitude but opposite in signs.
- Find the SUM of 20 terms of the series whose rth term is 3r + 1
- Resolve into Partial Fraction
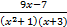
- Show that 16C11+ 16C10 = 17C11
- Find the term independent of x in the expansion of
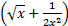
- If cotθ =
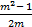 and 0 < θ <
and 0 < θ <  find the value of remaining trigonometric ratios.
find the value of remaining trigonometric ratios.
- If sinα =
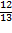 , then find the values of sin2α and cos2α, where 0 < α <
, then find the values of sin2α and cos2α, where 0 < α < 
- Draw the graph of y = tan x, x
 [-π,π] Graph paper should be given to the candidates.
[-π,π] Graph paper should be given to the candidates.
- Solve the triangle ABC if
α = 35°17' , β = 45°13', b, = 421
- Show that cos-1 (-x) = π –cos-1x
- Solve 2x - y = 4 and 2x2 - 4xy – y2 = 6
- Show that the statement
 q
q 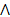 (p
(p  q)
q) 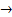
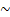 q is a tautology.
q is a tautology.
SECTION - C (Marks 40)
Note: Attempt any FIVE questions. All questions carry equal marks. (5 x 8 = 40)
Q.3 Prove that 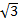 is an irrational number.
is an irrational number.
Q.4 Find the value of A for which the system has non-trivial solutions. Also find solution for
the value of 𝞴
x + y + z = 0
2x+y- 𝞴z = 0
x + 2y - 2z = 0
Q.5 Show that roots of the equation
(x-a)(x-b) + (x-b)(x-c) + (x-c)(x-a) = 0
are real and will be equal only if a=b=c
Q.6 If m and n are nearly equal show, that (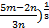
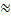
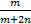 +
+ 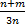
Q.7 If 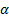 , β, γ are the angles of a triangle ABC, then show that
, β, γ are the angles of a triangle ABC, then show that
Cot  + Cot
+ Cot  + Cot
+ Cot  = Cot
= Cot  Cot
Cot  Cot
Cot 
Q.8 Prove that r1 =  with usual notation. Also show that r1 = s tan
with usual notation. Also show that r1 = s tan 
Q.9 Solve the equation sin2x + cosx = 1
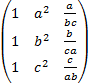 = 0
= 0