Inter (Part-I) Lahore Board 2012
Mathematics Paper I (Objective Type)
Time Allowed: 30 Minutes
Max. Marks: 20
(Group-I)
Note: Four possible answers A, B, C and D to each question are given. The choice which you think is correct, fill that circle in front of that question with Marker or Pen ink. cutting ear filling two or more circles will result in zero mark in that question. Write the letter A, B, C or D in the column (write correct option) against each question also. If there; is a contradiction in the bubble and hand written answer, bubble option will be considered correct.
Q1.
A. Natural number
B. Whole number
C. Rational number
D. Irrational number
A. 3i
B.
C.
D. -3i
A. 0
B. 1
C. 2
D.
A. 1
B. 2
C. 3
D. -4
A -A
B. A
C. At
D. A2
A. 7
B. 6
C.-6
D. 7
A.
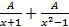
B.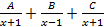
C.
D.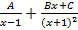
A.
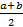
B. a + b
C. a-b
D.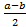
A. 0<x<

B.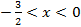
C. 1/2< x <-1/2
D. 0<x<
A. n!
B. (n+1)!
C. 0
D. n
A.

B. 1/3
C.
D.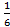
A.
B.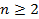
C.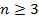
D.
A. T4
B. T5
C. T6
D. T7
A.
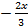
B.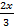
C.
D.
A. one degree
B. one radian
C. 180°
D. radians
A.
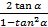
B.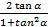
C.
D.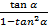
A.
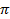
B. 7
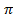
C.
D.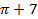
A. cos
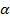
B. cos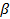
C. cos
D. sin
A.
B.
C. 1
D.
A. I and II quadrant
B. I and III quadrant
C. H and IV quadrant
D. I and IV quadrant
Inter (Part -I) Lahore 2012
Mathematics Paper I (Essay Type)
Time Allowed: 2.30 Hours Max. Marks: 80
(Group-I)
SECTION-I
Write short answers to any EIGHT (8) questions: 16
3. Write short answers to any EIGHT (8) questions
 and show that A-1A=I3
and show that A-1A=I3 6.A. Use synthetic division to find the values of p and q if x + 1 and x - 2 are the factors of the polynomial x3 + px2 + qx + 6 (5)
B. Find the 18th term of the A.P. if its 6th term is 19 and the 9th term is 31. (5)
7.A. Show that 16c11+16c10= 17C11 (5)
B. Find the coefficient of x5 in the expansion of ![]() (5)
(5)
8.A. If ![]() is arc length of a circle central angle of an arc is
is arc length of a circle central angle of an arc is ![]() radian and r is radius of a circle then prove
radian and r is radius of a circle then prove ![]() = r
= r![]() . (5)
. (5)
B. Prove that (without using calculator) cos 20° cos 40° cos 60° cos 80° = ![]() (5)
(5)
9.A.Solve the triangle ABC,in which a = 7, b = 7, c = 9 . (5)
B. Prove that (without using calculator) ![]()