PAPER CODE NUMBER:2195
(A)2012
ROLL NO…………………
INTERMIDIATE
PART-I(11TH CLASS)
MATHEMATICS
PAPER-I TIME ALLOWED :30 MIUTES
GROUP-1 OBJECTIVE MAXIMUM MARKS :20
NOTE:- you have four choices for each objective type question as A,B,C and D. the choice that you think is correct , fill the circle in front of the question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. attempt as many questions as given in objective type question paper and leave others blank. write the letter A,B,C or Din the column against each question. If there is a contradiction in the bubble and hand written answer, bubble option will be considered correct.
Q.NO.1
- if A and B are disjoint events then P(AVB) =
(a)P(A)
(b)P(B)
(c)P(A)+P(B)
(d)P(A)-P(B)
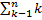 is equal to :-
is equal to :-
(a)n/2
(b)n+1/2
(c)n(n-1)/2
(d)n(n+1)/2
- the terms in the expansion of (1-x)2 are:-
(a)8
(b)7
(c)9
(d)10
- in one hour, the hour hand of the clock turns through an angle:-
(a)π/8
(b)π/6
(c)π/4
(d)π/2
- tan 2 θ =
(a)2tanθ/1+tan2θ
(b)tan θ/1-tan2θ
(c)2tanθ/1-tan2θ
(d)1-tan2θ/1+tan2θ
- period of tan x/3 is :-
(a)π
(b)π/2
(c)π/3
(d)3π
- cos(sin-1 1/
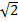 ) is equal to :-
) is equal to :-
(a)1/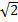
(b)1/2
(c)π4
(d)-π/4
- cos a/2 =
(a)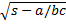
(b)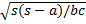
(c)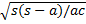
(d)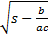
- in – radius r=
(a)Δ/s-a
(b)Δ/s-b
(c)Δ/s
(d)Δ/s-c
- the domain of principal cos function is :-
(a)-1
(b)1
(c)0
(d)[0,π]
- the number 22/7 is called a :-
(a)irrational number
(b)rational number
(c)integer
(d)natural number
- the set {(1,2)} is called:-
(a)infinite set
(b)singleton
(c)empty set
(d)ordered pair
- a square matrix M is singular if:-
(a)M=1
(b)M=-1
(c)M=0
(d)M=M
- if the matrices A and B are conformable for multiplication then (AB)’=
(a)AB
(b)A
(c)B
(d)B’A’
- the roots of the equation x2-x-2=0 are:-
(a)2,1
(b)1,2
(c)1
(d)-2
- the product of the four fourth roots of unity is:-
(a)1
(b)-1
(c)0
(d)2
- partial fraction of 1/(x+1)(x-2) are of the form:-
(a)A/x+1
(b)B/x-1
(c)A/x+1+B/x-2
(d)A/x+1+Bx+C/x-2
- G.M. between 2 and 8 is equal to :-
(a)2
(b)8
(c)16
(d)±4
- the sum of an infinite geometric series is equal to:-
(a)a/1-r
(b)a/1-r
(c)a/1-r2
(d)a/1+r2
- the value of n when Pn=11.10.9 is:-
(a)1
(b)3
(c)2
(d)0
2012
ROLL NO ……………
INTERMIDIATE PART-I( 11TH CLASS)
MATHEMATICS
PAPER-I TIME ALLOWED : 2.30 HOURS
GROUP-I SUBJECTIVE
MAXIMUM MARKS : 80
SECTION-I
NOTE: write same question number and its part number on answer book, as given in the question paper.2. Attempt any eight parts. 8 x 2 = 16
- simplify, justify each step 4 +16 x/4
- simplify (-1/2 -
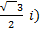 3
3
- write down the power set {9,11}
- write the converse, inverse of the condional ~ p→q
- for A= {1,2,3,4} find the relation {(x,y)/x+y>5}
- define the group.
- if A and B are square matrix of the same order , explain why in general
(A – B)2 = A2 – 2AB +B2
- show that 2 3 0 2 1 0 without expansion.
3 9 6 = 1 1 2
2 15 1 2 5 1
- if A= 1 1 +6 find (A)2
1 -i
- define the extraneous roots.
- evaluate ( 1 + ш – ш2)(1-ш+ш2)
- find two consecutive numbers whose product is 132.
3.attempt any eight parts. 8 x 2 = 16
- define proper rational fraction .
- resolve 2x +1/(x-1)(x+2) into partial fractions.
- if 1/a, 1/b, 1/c are in A.P, show that b= 2ac/a+c
- if y = x/2 + x2/4 + x3/8 +-------------- and 0<x<2, then prove that x = 2y/I +y
- define harmonic mean between a and b.
- write into factorial form the expression n(n-1)(n-2)
- find the number of diagonals of 12 sided polygon.
- define equally likely events.
- the probabilities that a man and his wife will be alive in the next 20 years are 0.8 and 0.75 respectively. Find the probability that both of them will be alive in the next 20 years.
- using mathematical induction , prove that 2+4+6+--------+ 2n=n(n+1) for n= 1 and n =2
- calculate ‘r’ for finding term independent of x in the expansion of (x/2 + 2/x2)12
- (xii)if x is so small that its square and higher powers be neglected, then prove that 1-x/
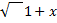
=1 – 3x/2
4.attempt any nine parts. 9 x 2 = 18
- find the values remaining trigonometric functions, if sinθ = 12/13 and terminal arm of the angle is in quadrant 1st .
- prove that identity : cot2θ –cos2θ = cot2θ cos2θ
- prove that : sin (180° + a) sin (90°- a) = sina cosa
- express in the form of r sin(θ + Ø) : 12 sinθ +5sosθ
- prove that cot a – tan a = 2 cot 2a
- express the following sum as product : sin5θ + sin3θ
- find the domain and range of y = tan x
- find the period of sinx/5
- solve the right angle triangle in which a = 3.28, h = 5.74, y =90°
- solve the triangle in which a = 32, b = 40, c = 66
- prove that r = b sin y/2 sin a/2 sec β/2
- find the solution which lies in [0,2π] cotθ = 1/

- find the solution set of the equation : sin4x-sin2x = cos3x
SECTION-II
NOTE : ATTEMPT ANY THREE QUESTIONS. 3 X 10 = 30
5.(a)construct the truth table of [(p→q)^ p] → q
(b)solve the system of linear equations by cramer’s rule.
2x +2y +z = 3, 3x-2y-2z=1, 5x +y-3z =2
6.(a)solve the equation (x-1/x)2 + 3(x+ 1/x) =0
(b)find five number in A.P whose sum is 25 and sum of whose square is 135.
7.(a)a die is thrown twice . what is the probability that the sum of number of dots shown is 3 or 11?
(b)if x is very nearly equal ,then prove that pxp –qx4 = (p-q) xp+q
8.(a)prove that sin6θ – cos6θ = (sin2θ –cos2θ)(1-sin2θ.cos2θ)
(b)prove that cos 20° cos40° cos60° cos80°= 1/16
9.(a)a kite flying at a height of 67.2 m is attached to a fully stratched string inclined at an angle of 55° to the horizontal. Find the length of the string.
(b)prove that tan-13/4 + tan-1 3/5 – tan-1 8/9 = π/4
PAPER CODE NUMBER :2196
(A)2012
ROLL NO…………..
INTERMIDIATE PART-I(11TH CLASS)
MATHEMATICS PAPER-I
TIME ALLOWED : 30 MINUTES
GROUP-II
OBJECTIVEMAXIMUM MARKS:20
NOTE:- you have four choices for each objective type question as A,B,C and D. the choice that you think is correct , fill the circle in front of the question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. attempt as many questions as given in objective type question paper and leave others blank. write the letter A,B,C or Din the column against each question. If there is a contradiction in the bubble and hand written answer, bubble option will be considered correct.
Q.NO.1
- The value of n, when C5=C4 is equal to :-
(a)5
(b)4
(c)8
(d)9
- a die is rolled, the probability that dots on the top are even is:-
(a)1/2
(b)1/3
(c)!
(d)none of these
- the expansion of (1+2n)-1 is valid if:-
(a)x<1
(b)x<1/2
(c)x=1
(d)x<2
- with usual notation ℓ equal to :-
(a)y
(b)θ
(c)yθ
(d)none of these
- cos 2θ =
(a)2tanθ/1-tan2θ
(b)2tan θ/1+tan2θ
(c)1-tan2θ/1+tan2θ(d)1+ tan2θ/1-tan2θ
- period of cos x/3 is :-
(a)π
(b)3π
(c)2π/3
(d)6π
- area of ΔABC =
(a)1/2 ab sin a
(b)ab sin y
(c)1/2 ac sinβ
(d)ab sin a
- radius of escribed circle opposite to vertex B is :-
(a)Δ/s
(b)Δ/s-a
(c)Δ/b
(d)Δ/s-b
- the domain of the principal tan function is :-
(a)[-π/2,π/2]
(b)(0,π)
(c)R
(d)(-π,π)
- the value of cos(tan-1θ) is equal to :-
(a)0
(b)1
(c)-1
(d)1/2
- ‘π’ is a :-
(a)rational number
(b)irrational number
(c)integer
(d)1/2
- the set {Ø} is called:-
(a)infinite set
(b)empty set
(c)singleton
(d)none of these
- a square matrix A is a skew hermitian if(A)’ is equal to:-
(a)A
(b)A
(c)At
(d)-A
- if the matrices A and B are conformable for multiplication then:-
(a)AB=BA
(B)AB=A
(C)AB=B
(D)AB=BA
- if ш is a cube root of unity then ш3 =
(a)ш
(b)ш2
(c)-1
(d)1
- the roots of ax2 +bx+c=0 are complex if :-
(a)b2 -4ac<n
(b)b2 -4ac=0
(c) b2 -4ac>0
(d)-1
- partial fraction of 1/x2 -1 are of the form :-
(a)Ax +B/x2 -1
(b)A/x-1 +B/x+1
(c)A/x-1
(d)B/x+1
- A.M between a and c is :-
(a)a-c/2
(b)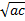
(c)a+c/d
(d)a+c/2
- the sum of an infinite geometric series exists if:-
(a)r>1
(b)r<1
(c)r=1
(d)r=-1
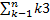 is equal to :-
is equal to :-
(a)[n(n+1)/2]
(b)n(n+1/2
(c)n(n-1/2
(d)n(n+1)(2n+1)/6
(A)2012
ROLL NO …………….
INTERMIDIATE PART-I(11TH CLASS)
MATHEMATICS PAPER-I
TIME ALLOWED : 2.30 HOURS
GROUP-II
SUBJECTIVE
MAXIMUM MARKS :80
NOTE : write same question number and its part number on answer book, as given in the question paper.
SECTION-I
2. attempt any eight parts. 8 x 2 = 16
(i) does the set {1,-1} possess closure property w.r.t multiplication?
(ii) find the multiplicative inverse of (-4,7).
(iii) write down the power set of {+,-,x,÷}
(iv)construct the truth table of (p^~p)→q.
(v) prepare a table of addition of the elements of the set of residue classes module 4.
(vi)define group.
(vii) find x and y if x+3 1 = y 1
-3 3y-4 -3 2x
(viii) if A= 1 2 -3 , then find A12 and A32
0 -2 0
-2 -2 1
(ix)if A is symmetric, show that A2 is symmetric.
(x)define extraneous root of an equation.
(xi) prove that sum of cube roots of unity is zero.
(xii)discuss the nature of roots of the equation x2 -5x + 6 = 0
3. attempt any eight parts. 8x2=16
(i) resolve into partial fraction 3x2+1/x-1
(ii) write !st four terms an – an-1 = n+2 where
(iii) find A.M between x-3 and x+5.
(iv) find the 9th term of the sequence -1/5, -1/3.-1,----------
(v) find the value of n when Pn =11, 10, 9
(vi) how many diagonals can be formed by joining the vertices of the polygon having 8 sides?
(vii) a die is rolled . what is the probability that the dots on the top are greater then 4?
(viii) how many arrangements of the letters of the word “PAKISTAN” taken all together can be made?
(ix) expand (1+x)-1/3 upto 4 terms.
(x) show that 1---------------+(4n-3)=n(2n-1) for integral values of n>0.
(xi) find the arms involving x2in the expansion of (x-2/x2)13
(xii) define the rational fraction.
4. attempt any nine parts. 9 x 2 = 18
(i) discuss the signs of trigonometric functions in III and IV quadrant.
(ii) prove that tanθ+cotθ= cosecθ secθ.
(iii) without using calculator find tan (1110°).
(iv) show that tan(45°+A) tan(45°-A)=1
(v) if cos a=3/5, find sin2a when 0 < a <π/2
(vi) express 2 sin3θcosθ as sum or difference.
(vii)write the domain and range of y=cosx
(viii)find the period of sin3x.
(ix) in right triangle ABC, find a if b= 30.8, c=37.2, y=90°
(x) write the law of sine.
(xi) show that r1 =s tan a/2
(xii) find the solution of sec x = -2 in[0,2π]
(xiii) find the value of θ if 2sin2θ –sinθ= 0
SECTION-II
NOTE : attempt any three questions. 3 x 10 = 30
5.(a) give logical proof of the theorem (AпB)’ = A’UB’
(b) show that x 1 1 1
1 x 1 1 = (x+3)(x-1)3
1 1 x 1
1 1 1 x
6.(a) show that the roots of (mx+c)2 =4ax will be equal , if c = a/m
(b) find three consecutive numbers in G.P whose sum is 26 and their product is 216.
7.(a) two dice are thrown twice. What is the probability that the sum of dots shown in the first throw is 7 and that of the 2nd throw is 11.
(b) if 2y = 1/22 + 1.3/2! . 1/24 + 1.3.5/3! . ½6+------------- then prove that 4y2 +4y-1=0
8.(a) prove that ℓ =r θ
(b)prove that cos(90°+θ).sec(-θ ). Tan(180°-θ)/sec(360°-θ).sin(180°+θ).cot(90°-θ) =
9.(a)solve the ΔABC in which b= 14:8, c= 16.1 and a =42°45’
(b)prove that sin-1 1/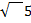 +cot-1 3 = π/4
+cot-1 3 = π/4
2012(S) ROLL NO…………
INTERMIDIATE PART –I(11TH CLASS)
MATHEMATICS PAPER-I
TIME ALLOWED :30 MINUTES
OBJECTIVE MAXIMUM MARKS :20
NOTE:- you have four choices for each objective type question as A,B,C and D. the choice that you think is correct , fill the circle in front of the question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. attempt as many questions as given in objective type question paper and leave others blank. write the letter A,B,C or Din the column against each question. If there is a contradiction in the bubble and hand written answer, bubble option will be considered correct.
Q.NO.1
- The probability of an event can never be :-
(a)1
(b)0
(c)-1
(d)1/2
the inequality 4n > 3n +2n-1 is true for integral values of n if
(a)n>0
(b)n≥1
(c)n≥2
(d)n≤2
- the sum of co efficient In the expansion of (1+x)n is :-
(a)2n-1
(b)2n+1
(c)2n-2
(d)2n
- the no of terms independent of x in the expansion of (x/2+2/x2)12 is :-
(a)5
(b)6
(c)7
(d)8
- (1-sinθ) (1+tanθ) =
(a)cosθ
(b)-1
(c)sec θ
(d)1
- 4 cos a -3 cos a =
(a)sin 3 a
(b)cos 3a
(c)cos 2 a
(d)sin 2 a
- period of cot 8x is :-
(a)8π
(b)π/4
(c)π/8
(d)π
- ab sin y =
(a)area of triangle ABC
(b)1/2 area of triangle ABC
(c)2 area of triangle ABC
(d)3 area of triangle ABC
- domain of y= cosec-1 x is :-
(a)x≤-1 or x≥ 1
(b)(-π/2,π/2)
(c)R
(d)-1≤x≤1
- if sin x = ½, then reference angle is :-
(a)π/6
(b)π/3
(c)π/4
(d)-π/6
- reflexive property is :-
(a)a=a
(b)a=b→b=a
(c)a=b b=c a=c
(d)a=b→a+c=b+c
multiplicative inverse of (1,0) is :-
(a)-1,0
(b)0,1
(c)0,-1
(d)1,0
- contrapositive of ~p→q is :-
(a)q~→p
(b)q→~p
(c)~q→p
(d)q→p
- if a,b G and G is a group , then (ab)=-1
(a)a-1 b-1
(b) b-1 a-1
(c)-1/ab
(d)1/ab-1
- a square matrix A = (a) is upper triangle:-
(a)a =0 i=j
(b)a= o i>j
(c)a=0 I <j
(d)a=0 i>j
- if a,β are roots of ax2 +bx +c=0, then a +β=
(a)c/a
(b)-b/a
(c)a/c
(d)a/b
- x2+x-6=0 is :-
(a)conditional equation
(b)identity
(c)proper fraction
(d)improper fraction
a sequence {a} is an arithematic sequence if nЄN and n>1
(a)an/an-1 is same
(b)an –an-1 is same
(c)an+1 –an-1 is different
(d)none of these
- G.P. is :-
(a)1,3,5
(b)1,3,9…..
(c)1,1/3,1/8…….
(d)1,1/3,1/5…….
- Pn =
(a)1
(b)n!
(c)0
(d)n
2012(S)
ROLL NO …………..
INTERMIDIATE PART-I(11TH CLASS)
MATHEMATICS
PAPER-I TIME ALLOWED : 2.30 HOURS
SUBJECTIVE
MAXIMUM MARKS:80
NOTE : write same question number and its part number o answer book, as given In the question paper.
SECTION-I
2. Attempt any eight parts. 8 x 2 = 16
- sequence 2-7i/4+5i into real and imaginary parts.
- simplify i101
- write the inverse and contrapositive of q→p
- define a monoid.
- under what conditions on sets A and B monoid the statements A-B= A is true?
- evaluate determinant of A = 1 -2 3
-2 3 1
-4 -3 2
- if A = 1 2 and A2 = 0 0 , find values of a and b.
A b 0 0
- find the condition that one root of x2 +px +q=0 is additive inverse of the other.
- discuss the nature of the roots of 2x2 +5x-1=0
- show that x – 2 is a factor of x2 -7x + 10 = 0 by factorization.
3.attempt any eight parts. 8 x 2 = 16
- resolve into partial fraction 2x +1/(x-1)(x+2)(x+3)
- resolve into partial fraction 4x/ (x+4)2(x-1)
- which term of the A.P 5.2 -1, is -85.
- insert two G.M between 1 and 8.
- if a = -1/3 of H.P.a5 = 1/5 of H.P, find 9th term of H.P.
- find the value of n. p1 =30
- find the value of n. C10 = 12x11/2!
- a dice is thrown. Find the probability that the dots on the top are prime numbers or odd numbers.
- a natural number is chosen out of first fifty natural numbers. What is the probability that chosen number is multiple of 3 or of 5?
- use mathematical induction to prove the formula V+ve inmteger of n
1+5+9+………+(4n-3)= n(zn-1)
- find the term involving x-2 In the expansion of (x- 2/x2 )13
- expand upto 4 terms (8-2x)-1
4.attempt any nine parts. 9 x 2 = 18
- define co-terminal angles.
- prove that sin2 π/6 + sin2 π/3 + tan2 π/4 =2
- write expansion of tan(a-β) and tan (a+β)
- prove that sin(a-β)+sin(a-β)/cos(a+β)+ cos(a-β) is tan x
- show that cot a – tan a = 2 cot 2a
- verify that sin 8 x + sn 2x/cos 8x – cos2x = tan 5x
- write the domain and range of cot x
- find the period of sin x/5
- a vertical pole is 8m high and length of its shadow is 6m. find the angle of elevation of sun at hat moment.
- if in a ΔABC, a=93; c= 101; β= 80° find b
- find the area of ΔABC when a= 200; b= 120, y = 150°
- what is trigonometric equation? Give one example.
- solve the trigonometric equation? Cosec θ = 2 over[0,2π]
SECTION-II
NOTE : attempt any three questions. 3 x 10 = 30
5.(a)determine whether (P(S)) where stands for intersection, is a semi group monoid or neither. If it is a monoid, specify its identity.
(b)solve the following system of linear equations by cramer’s rule.
2x+2y+z=5
3x – 2y-2z=1
5x +y 3z = 2
6.(a)the sum of an infinite geometric series is 9 and the sum of the squares of its terms is 81/5.
Find the series.
(b)find the three cube roots of -27.
7.(a)how many diagonals can be formed by joining the mvertices of polygon having 5 – sides.
(b)if y=1/3 + 1.3/2! (1/3)2 + 1.3.5/3!(1/3)2 ………….. prove that y2 + 2y -2=0
8.(a)if tanθ= 1/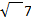 and terminal arm of the angle is not in the III quadrant .
and terminal arm of the angle is not in the III quadrant .
Find the value of cosec2θ-sec2θ/cosec2θ+sec2θ
(b)prove that : sin 3θ/cosθ +cos3θ/sinθ = 2 cot2θ
9.(a)solve the triangle ABC if c= 16.1, a= 42° 45’, y =74° 32’
(b)prove that sin-15/13 +sin-1 7/25 – cos-1 253/325