Paper Code
Number:4195
2012(A)
ROLL.NO: ____________
INTERMEDIATE PART-II (12TH CLASS)
MATHEMATICS PAPER –II GROUP-I
TIME ALLOWED:30
MAXIMUM MARKS:20
OBJECTIVE
Note: You have four choices for each objective type question us A, B, C and D. The choice which you think is correct, fill that circle in front of that question number. Use marker or pen to fill the circles, Cutting or filling two or more circles will mull in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case
BUBBLES are not filled. Do not solve question on this sheet of OBJECTIVE PAPER.
Q.No.1
- If f(x) =
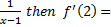
a. 1
b. 0
c. -1
d .2

a. -ln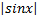 +c
+c
b.-ln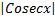 +c
+c
c. ln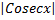 +c
+c
d. ln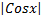 +c
+c
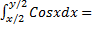
a. 0
b. 1
c. -2
d. 2
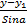 =
= 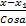 is called
is called
a.Intercept form
b.Point-slope form
c.Symmetric form
d. Normal form
- Equation of a straight line passing through P(a,b) are parallel to x-axis is:
a. X=a
b. Y=b
c. X=b
d.Y=a
- For the in equalities 2x+y ≤10 and x+4y ≤12, the corner point is:
a. (5,10)
b. (12,3)
c. (4,2)
d. (10,12)
- In ellipse
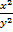 +
+ 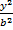 = 1; coordinates (a ±b) represents.
= 1; coordinates (a ±b) represents.
a. Verticies
b. Co-vertices
c.Foci
d.Origin
- The point of parabola which is closet to the focus is:
a.Verticies
b. Co-vertices
c.Foci
d.Origin
- Equation of the tangent to the circle
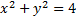 at (
at (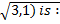
a. X+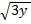 =4
=4
b.X- =4
=4
c. -y = 4
-y = 4
d. 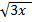 + y = 4
+ y = 4
- Volume of parallelepiped =
a. 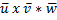
b. 
c. 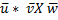
d.  (
( )
)
- Two vectors
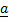 and
and  are coplanner if p
are coplanner if p = 0 implies:
= 0 implies:
a. P=0, q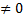
b. P=0,q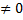
c. P=0 , q = 0
d. P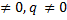
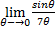 =
=
A.1
B. 7
C. 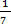
D. Undefined
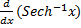 =
=
a. 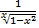
b.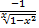
c. 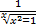
d. 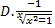
NOTE: WRITE SAME QUESTION NUMBER AND ITS PART NUMBER ON ANSWER BOOK, AS GIVEN IN THE QUESTION PAPER.
SECTION-I
ATTEMPT ANY EIGHT PARTS. 8 X 2 = 16
- Prove that sin h 2x = 2 sin h x cos h x
- Evaluate
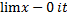 x/tan x
x/tan x
- Differentiate x2 +1/x2-3 w.r.t ‘x’
- If xy +y2=2 then find dy/dx
- Find dy/dx if x=y sin y
- Differentiate w.r.t ‘x’ 1/a sin-1 a/x
- Prove that d/dx(sin h x) = cos h x
- If f(x) = et (1+ℓnx), find f(x)
- If y = cos3 x, find y2
- Find the slope of tangent at (4,2) to the graph x2 –y2 -6y=0
- If y = sin 3x, find y4
- Define the stationary point for the function f (x)
3. Attempt any eight parts. 8 x 2 = 16
- Integrate ∫(
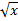 + 1/
+ 1/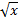 ) dx.
) dx.
- Integrate ∫ x2/4 + x2 dx.
- Integrate ∫ x3 ℓnx dx.
- Integrate ∫ex(1/x + ℓnx) dx.
- Evaluate ∫ 2x/ x2 –a2 dx.
- Prove that ∫ f(x) dx = ∫ f (x) dx +∫ f(x) dx
- Evaluate ∫ ( x1/3 + 1) dx
- Find the area bounded by cos x function from x = -π/2 to x = π/2
- Solve the differential equation dy/dx = -y
- Show that the points A (3,1), B(-2,-3) and C(2,2) are vertices of an isosceles triangle.
- The two points P and O1 are given in xy – coordinate system. Find xy-coordinate of P reffered to O1 x and O1 y where P(3,2), O1(1,3)
- Find slope and inclination of the line joining the points (-2,4),(5,11)
ATTEMPT ANY NINE PARTS. 9 X 2 = 18
- Find the distance between the points A (3,1); B(-2,-4)
- The coordinates of a point p are (-6,-8). The axes are translated through O (-4,-6).
- Define the x – intercept and y – intercept of O line.
- Find the point of intersection of lines x -2y +1 =0 and 2x – y+2=0
- Find the centre and radius of the circle x2+y2+12x – 10y =0
- Find the length of tangent from point P(-5,10) to the circle 5x2+5y2 +14x+12y-10=0
- Find the length of the chord cut off from the line 2 +3y =13 by the circle x2+y2=26
- Find the focus and vertex of the parabola x2 = 5y.
- Find the vertices and co-vertices of the ellipse x2 +4y2 = 16
- Find the eccentricity of the hyperbola y2/16 – x2/49 = 1
- Find the direction cosines of the vector V =4i -5j
- Find a real number a so that the vectors U=ai + 2 a j – k andV = I + a j +3 k are perpendicular
- Find a vector which is perpendicular to the plane containing a = -I –j –k, b = 2i -3j + 4k
SECTION-II
NOTE: ATTEMPT ANY THREE QUESTIONS. 3 X 10 = 30
5. (a)discuss the continuity of f (x) at x = 2 if f (x) = {x2 -1; if -2<x<2
(b) If y = (cos-1 x)2 , show that (1-x2) y2 –xy1 -2 =0
6. (A) evaluate ∫ i-sin x/1-cos x ex dx
(b) Find an equation of the line through (-4, 7) and parallel to the line 2x-7y+4=0
7. (A) find area bounded by the curve f (x) = x3-2x2+1 and the x – Axis in 1st quadrant.
(b) Maximize the function defined as f (x,y) = 2x+3y subject to the constraints
2x +y≤ 8, x +2y ≤ 14, x≥ 0 y≥ 0
8. (a) show that the circles x2 +y2 +2x -2y-7 = 0 and x2 +y2 -6x +4y +9=0 touch externally.
(b) Prove that line segment joining the mid points of two sides of a triangle is parallel to third side and half as long
9. (A)find the equation of parabola having focus (-3,1) and directory x -2y -3 = 0
(b) Prove that vectors i-2j+3k, -2i+3j -4k and I -3j +5k are coplanar.
Paper Code
Number:4195
2014(A)
ROLL.NO: ____________
INTERMEDIATE PART-I (12TH CLASS)
MATHEMATICS PAPER –II GROUP-I
TIME ALLOWED:30
MAXIMUM MARKS:20
OBJECTIVE
Note: You have four choices for each objective type question us A, B, C and D. The choice which you think is correct, fill that circle in front of that question number. Use marker or pen to fill the circles, Cutting or filling two or more circles will mull in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case
BUBBLES are not filled. Do not solve question on this sheet of OBJECTIVE PAPER.
Q.No.1
NOTE: write same question number and its part number on answer book, as given in the question paper.
SECTION-I
2. attempt any eight parts. 8 x 2 = 16
- determine whether the given function is even or odd f(x) = x3 +x
- evaluate (1-1/n)
- define the derivative of the function at the point x = a
- find the derivative of (ax +b)3 by first principle.
- differentiate x4+2x3 +x2 with respect to x.
- find dy/dx if 3x +4y +7=0
- differentiate (sin2θ- cos3 θ)2 with respect to θ.
- find f(x) for f (x) = e (1+ℓnx)
- find y2 for y =
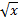 + 1/
+ 1/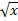
- apply maclaurim series expansion to prove that e2x = 1 + 2x + 4x2/2! +-------------
- find the extreme values for f (x) = x2 –x -2
- using differentials, find dy/dx for x4 + y2 = xy2
3. attempt any eight parts. 8 x 2 = 16
- find y and dy in y =x2 +2x when x changes from 2 to 1.8
- evaluate ∫ (
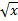 + 1)2 dx
+ 1)2 dx
- evaluate ∫x+b/(x2+2bx +c)1/2
- integrate x2 sin x by parts.
- evaluate ∫ e-x (cos x – sin x) dx.
- evaluate ∫ 2a/x2 –a2 dx, x>a
- evaluate ∫ 1/(2x -1)2 dx
- evaluate ∫ x
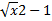 dx
dx
- find the area below the curve y= 3
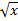 and above the x axis from x =1 to x = 4
and above the x axis from x =1 to x = 4
- solve the D.E (ex + e-x) dy/dx= ex – e-x
- indicate the solution set of linear inequalities x +y ≥ 5 and –y + x ≤ 1
- graph the system of inequalities x -2y ≤ 6, 2x +y≥ 2
4. attempt any nine parts. 9 x 2 = 18
- find points trisecting the join of A(-1,4), B (-6,2)
- two points P and O are given in xy- coordinate system. Find the X,Y co-ordinates of P refered to the translated axes OX and OY.P(-6,-8) O(-6,-4)
- what do you mean by the constants used in xcos a + ysina = p?
- if ℓ1 ℓ2 ; then show that m1 = m2.
- find the centre and radius of circle x2 +y2 -6x +4y+13 =0
- write down the equation of tangent to the circle x2 +y2 =49 at (4,3)
- define hyperbola.
- find focus and vertex of the parabola y2 = 2x
- find the centre and foci of the ellipse 9x2 +y2 =18
- find the equation of hyperbola having foci at (0,6) and e =2
- find –u +v+w; where u = 2i -7j; v =i-6j, w = -I +j
- find cosine of angle where x = 3i +5j; y =6i + 2i
SECTION-II
NOTE : attempt any three questions. 3 x 10 = 30
5.(a) find the values of m and n, so that given function f(x) is continuous at x = 3
(b)differentiate (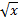 +1)(x3/2 -1)/x3/2 x3/2 with respect to x.
+1)(x3/2 -1)/x3/2 x3/2 with respect to x.
6.(a)evaluate ∫ x dx/x4 + 2x2 +5
(b) prove that distance of the point p(x1,y1) from the line ax +by +c = 0
7.(a) find the area between the X – axis and the curve y = 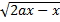 a>0
a>0
(b) minimize z = 2x +y subject to the constraints x+y≥ 3, 7x +5y≤ 35, x≥ 0, y ≥ 0
8.(a)find the equation of circle passing through A (3,-1), B(0,1) and having centre at 4x -3y -3 = 0
(b) use vectors to prove that diagonals of a parallelogram bisect each other.
9.(a) find the focus vertex equation of directrix and magnitude of the latusrectum of the parabola x2 -4x -3y +13 = 0
(b) prove by vector method that the angle in a semicircle is a right angle.
![]()
![]()
![]()
![]() +1)(x3/2 -1)/x3/2 x3/2 with respect to x.
+1)(x3/2 -1)/x3/2 x3/2 with respect to x.![]() a>0
a>0