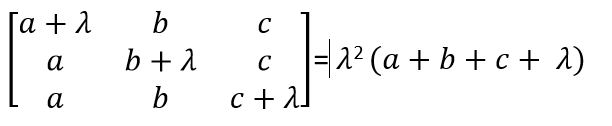RAWALPINDI BOARD 2012
PAPER Mathematics PART-I
(Objective Part)
Marks: 20

Note: You have four choice for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.

• Set of rational numbers is denoted by

(A) Q
(B)
(C)
(D)

• Modulus of complex number a + ib is

(A)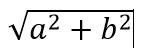
(B)
(C)
(D)

• Proposition p →q is called converse of

(A) p →q
(B)
(C)
(D)

• Which of the following is uninary operation?

(A) Square root
(B)
(C)
(D)

• If A is a matrix of order 3 x 2 , then the order of A^t is

(A) 2 x 3
(B) 3 x 3
(C) 2 x 2
(D) 3 x 2

• Product of roots of 2x² - 4x + 2 = 0 is

(A) -1
(B) 1
(C) 2
(D) -2

• Partial fraction of 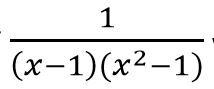 will be of form 

(A)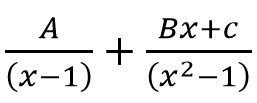  
(B)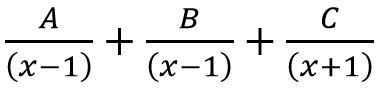
(C)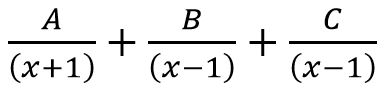
(D)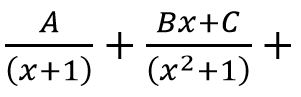

• If a_n-3=2 - 5 , then the nth term is

(A) 2n + 1
(B)
(C)
(D)

(A) n(n+1)/2
(B)
(C)
(D)

• ⁿC_n =

(A) 1
(B)
(C)
(D)

A die is rolled, then n(s) =

(A) 6
(B)
(C)
(D)

• (a + b )⁵ contains

(A) 5 terms
(B) 6 terms
(C) 7 terms
(D) 4 terms

• In expansion of (x + y)¹⁰ middle term is

(A) T₆
(B) T₅
(C) T₇
(D) T₄

• The sum of even coefficients in expansion (1 + x )⁴ is

(A) 16
(B) 12
(C) 10
(D) 8

• If tan 0 > 0 , sin 0< 0 , then terminal arm of angle lies in

(A) III quadrant
(B)
(C)
(D)

• cos(π+0) =

(A) -cosθ
(B)
(C)
(D)

• Period of tanθ  is

(A) π
(B)
(C)
(D)

• Δ/s=

(A)  r
(B)
(C)
(D)

• cos (tan^-1 0)=

(A) 0
(B) 1
(C) - 1
(D) ∞ 

• If sec x = -2 , then  x =

(A) 2π/3 , 4π/3
(B)
(C)
(D)

Inter (Part-I) Rawalpindi Board 2012
Mathematics
Part I (Subjective)
Time Allowed: 3.10 Hours 
Max. Marks: 83

SECTION-I

2. Attempt any EIGHT short questions.

• State the transitive property of equality of real number R
• Show that ∀z ε c, z+z^-2 is a real number.
• Define equal sets.
• Show that the statement (p ∧ q) → p is a tautology
• For = {1,2,3,4}, find the relation in A. if  A = {(x,y) = | y + x = 5} 
• Prove that in a group G, inverse of each element is unique.
• Solve the matrix equation for X : As 3X - 2A = B ,
  If  and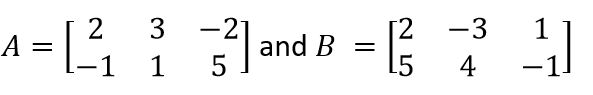
• Define skew -symmetric matrix.
• Solve x^-2-10 = 3x^-1
• State the Remainder Theorem.
• Find two consecutive numbers, whose product is 132.
• Show that =

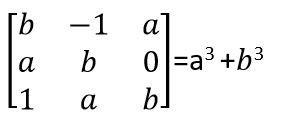
3. Attempt any EIGHT short questions.

• Resolve into partial fractions.
• Resolve into 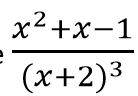partial fractions.
• Insert two GMs between 2 and 16.
• Prove that ⁿC_r =ⁿ C_n-r
• Prove that: P(E) = 1 - P(E) 
• Check whether n³ - n is divisible by 6 or 4.
• Prove that G² =, where A,G,H, are arithmetic, geometric and harmonic means respective.
• How many 3 digit numbers can be formed by using each one of the digits 2, 3, 5, 7. 9 only once?
• How many terms of the series -7 + (-5) + (-3) +…….. amount to 65?
• A dice is thrown. Find the probability that the dots on the top are prime numbers or odd numbers.
• Find 6th term in the expansion of ¹⁰
• Expand (2 -3x)^-2 up to 3 terms.

4. Attempt any NINE short questions.

• Define a degree.
• With usual notation prove that θ= r θ.
• Verify cos 2θ  =1 - 2 sin²θ for  θ=30°
• Show that: (secθ  + tanθ ) (secθ  - tanθ ) =1
• Prove that tan (45° + A) tan(45° - A ) = 1
• Express cos(x+y) sin(x-y)  as a sum or difference.
• Draw the graph of cos x from θ ° to 90° .
• Write any two formula of sine of half angles.
• Find the area of the ΔABC  in which b=21.6, c=30.2, a=52'
• Prove that in an Equilateral triangle r : R =1: 2
• Show that: cos(sin^-1x)=√1-x²
• With usual notation show that  = r=Δ/s
• Solve the equation: 1 + cosx  - 0

SECTION-II

Attempt any THREE questions.. (8 X 3 = 24)

Question #5 
a) Prove that: p˅( ˜pΛ˜̃˜̃pΛ˜̃q)q)(p˅q) = p˅
b) Show that