RAWALPINDI BOARD 2012
PAPER Mathematics PART-I
(Objective Part)
Marks: 20
Note: You have four choice for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.
(A) 1
(B)
(C)
(D)
(A)
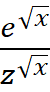
(B)
(C)
(D)
(A) -cosechx, cothx
(B)
(C)
(D)
(A) -1/2x
(B)
(C)
(D)
(A)
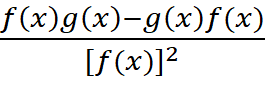
(B)
(C)
(D)
(A) d/dx (cosx)
(B)
(C)
(D)
(A) cotx + c
(B)
(C)
(D)
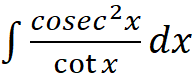 =?
=?(A) ln|tanx| + c
(B)
(C)
(D)
(A)
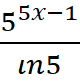
(B)
(C)
(D)
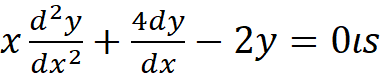
(A) 2
(B)
(C)
(D)
(A) -ecosx + c
(B)
(C)
(D)
(A) (1/2)ex2 + c
(B)
(C)
(D)
(A) 2/5
(B)
(C)
(D)
(A) y =7
(B)
(C)
(D)
(A) Infinite
(B)
(C)
(D)
(A) Parabola
(B)
(C)
(D)
(A)
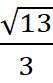
(B)
(C)
(D)
(A) Ellipse
(B)
(C)
(D)
(A)
x
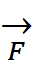
(B)
(C)
(D)
(A) cos-1
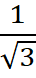
(B)
(C)
(D)
Inter (Part-I) Rawalpindi Board 2012
Mathematics
Part I (Subjective)
Time Allowed: 3.10 Hours
Max. Marks: 83
SECTION-I
2. Attempt any EIGHT short questions.
3. Attempt any EIGHT short questions.
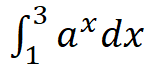
4. Attempt any NINE short questions.
Find the inclination and slope of the line joing of given A(-1,4), B(6,2).
2) Two points P and 0' are given in xy-coordinates system. Find the x,y coordinates of P referred to Coordinates axis O'X & O'y: P (3/2 , 5/2) , O'(-1/2 , 7/2)
3) What do you mean by constants used in xcosα+ysinα=p
5) Find the centre and radius of circle: x²+ y²+ 6x - 4y + 13 = 0
6) Write down the equation of tangent to the circle x² + y² = 64 at (4,3)
7) Define Hyperbola.
8) Find focus and vertex of parabola x² = 24
9) Find the centre and foci of ellipse x² + 9y² = 18
10) Find equation of hyperbola having Foci (0 , ±9) and Directories y=±4
11) Find ![]() , where
, where ![]() = 2
= 2![]() -
- ![]() ,
,![]()
12) Find the cosine of the angle between ![]() and
and ![]() where
where ![]() =
= ![]()
![]()
![]()
13) Find a unit vector ⊥ ![]()
![]() where
where ![]() =
= ![]() +
+ ![]() ,
,![]() =
= ![]()
SECTION-II
Attempt any THREE questions.. (8 X 3 = 24)
Question #5
a) Find the ![]()
b) If y =x4 + 2x² + 2 ,prove that ![]()
Question #6
a) Evaluate: ![]()
b) Transform the equation 5x - 12y + 39 = 0 into two Intercept form and normal form.
Question #7
a) Evaluate: ![]()
![]() 2
2![]()
![]() 2
2![]()
![]() .
.
b) Minimize Z = 2x + y subject to constraints x + y ≥ 3, 7x + 5y ≤ 5 , x ≥ 0 , y ≥ 0
Question #8
a) Find the coordinates of the points of intersection of the line 2x + y = 5 and the circle x²+y²+2x-9 = 0
b) CFind a vector of length 5 in the direction opposite that
of ![]() î - 2ĵ + 3ǩ
î - 2ĵ + 3ǩ
Question #9
a) Show that the equation 9x² - 18x + 4y² + 8y - 23 = 0 represents an ellipse. Find its elements.
b) Prove that in any triangle ABC c² = a²+b²-2abcosc