(12th CLASS-2013)
MATHEMATICS
GROUP FIRST
OBJECTIVE
TIME: 30 MINUTES
MARKS: 20
NOTE: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct, fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.
Q. NO. 1
(A) e-1
(B) e
(C) e2
(D) e3
(A) 4x + 1
(B) 4x + 3
(C) 4x – 3
(D) 4x -1
(A) sech x tanhx
(B) -Cosechx
(C) -Cosechx cothx
(D) -Coth2x
(A) 1/2
(B) 2/3
(C) 1/3
(D) 3
(A) –nxn-1
(B) nxn-1
(C) (n-1)xn-1
(D)
(A) n(f(x))n-1
(B) (f’(x))n
(C) n(f(x))n-1f’(x)
(D)
(A) e
(B) ex
(C)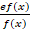
(D) ef(x)f’
(A)
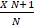
(B)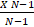
(C) nxn-1
(D)+ c
(A) aeax f(x) + c
(B) eax f’(x) + c
(C) eax f(x) + c
(D) aeax f’(x) + c
(A) 0
(B) -1
(C) 1
(D) ∞
(A) 0
(B) 6
(C) 8
(D) 16
(A) In/f(x)/+ c
(B) In/f’(x)/ + c
(C) ef’(x) + c
(D) ef(x) + c
(A) xy = c
(B) In/xy/= c
(C) In│x/y│= c
(D) x/y = c
(A)
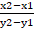
(B)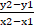
(C)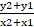
(D)
(A) x/a – y/b = 0
(B) x/a + y/b = 0
(C) x/a – y/b = 1
(D) x/a + y/b = 1
(A) 2x+ 3 > 0
(B) 2x+3 < 0
(C) x+ 4 > 0
(D) x+5 > 0
(A) (-1, -1)
(B) (-5, -3)
(C) (0, 0)
(D) (1, 1)
(A) (±a, 0)
(B) (0, ±a)
(C) (0, ±ae)
(D) (±ae, 0)
(A)
(B)
(C)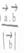
(D)
(A) 5
(B) 4
(C) 2
(D) 1
(12th CLASS 2013)
MATHEMATICS
SUBJECTIVE
GROUP FIRST
SECTION-I
2. Attempt any eight (8) short questions (16)
3. Attempt any eight (8) short questions (16)
4. Attempt any Nine (9) short question: (18)
Note: Attempt any three questions from this section 3 x10=30
5.(a) Show that ![]()
(b) Differentiate ![]() w.r.t, from first principles
w.r.t, from first principles
6 (a) Evaluate ʃ![]() dx
dx
(b) Find the equation of the line through the point (2, 9) and the intersection of the lines 2x + 5y – 8 =0 and 3x - 4y - 6 =0
7.(a) Evaluate ![]()
(b) Maximize f(x, y)= 2x+5y subject to the constraints
2y – x ≤ 8
X – y ≤ 4
X ≥ 0
Y ≥ 0
8.(a) Write an equation of circle that passes through points A(4,5) , B(-4,-3), C(8,-3)
(b) Define direction cosines of a vector and prove Cos2 α + Cos2 β + Cos2 γ = 1
9.(a) Show that the parabola (x Sinα - y Cosα)2=4a (x Cosα - y Sinα) has focus at (aCosα, aSinα) and the directrix xCosα + ySinα = 0
(b) Find volume of tetrahedron whose vertices are A(2,1,8), B(3,2,9), C(2,1,4) and D(3,3,10)