(a) π
(b) 2π
(c) ![]()
(d) - ![]()
FAISALABAD BOARD 2013
MATHEMATICS
PART-I
Time: 20 Min.
(Objective Part)
Marks: 17
Note: You have four choice for each objective type question as A,B,C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.
(a) π
(b) 2π
(c)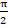
(d) -
(a)

(b) -
(c) 300
(d) 600
(a) Law of sines
(b) Law of cosine
(c) Law of tangents
(d) Hero formula
(a) Cos α
(b) Cos β
(c) Sin α
(d) Sin β
(a) π
(b) 2π
(c)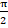
(d) -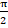
(a) 2Sin
Cos

(b) SinCos

(c) 2Sin+ Cos

(d) Sin+ Cos
(a) Identity
(b) Equation
(c) Fraction
(d) Formula
(a) 140
(b) -120
(c) 120
(d) 120
(a) A-1B-1
(b) B-1 A-1
(c) AB
(d) A-1 B
(a) 45°
(b) 90°
(c) 270°
(d) 360°
(a)
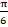
(b)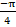
(c)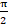
(d) - π
(a) Cos α
(b) Cos ẞ
(c) Sin ϒ
(d) Sin ẞ
(a) -
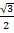
(b)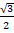
(c)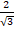
(d) 0
(a) 0
(b) 3
(c) 2
(d) 4
(a) 4
(b) 6
(c) 7
(d) 8
(a) -a > 0
(b) 2a < 0
(c)> 0
(d)
(a) x+ 1
(b) x-1
(c) x- 3
(d) x+ 5
(a) 3600
(b) 3350
(c) 2700
(d) 2250
(a)

(b) -
(c) 2
(d) -2
(a)π
(b)2π
(c)3π
(d)None
(a) Two middle terms
(b) 3 middle terms
(c) 4 middle terms
(d) 0 middle terms
Time: 3:10 Hours
(Subjective Part)Marks: 83
Section II
2. Attempt any EIGHT short questions. (8 x 2 = 16)3. Attempt any EIGHT short questions. (8 x 2 = 16)
4. Attempt any NINE short questions. (9 x 2 = 18)
Attempt any THREE questions. (8 x 3 = 24)
5. (a) Show that the set {1,ω ,ω2} when ω3 = 1 is an abelian group w.r.t ordinary ultiplication.
(b) Find inverse of the matrix, A = 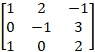
6. (a) Show that (1 + ω )(1+ ω2)(1 + ω4)(1+ ω8)……….2n - factors = 1 where is cube root of unity.
(b) Resolve into partial fraction ![]() .
.
7. (a) Find n so that may be H.M. between 'a' and 'b'.
(b) If if y = ![]() +
+ ![]()
![]() +
+ ![]()
![]() + ……….. prove that y2 +2y -2 = 0.
+ ……….. prove that y2 +2y -2 = 0.
8. (a) If cosec θ = ![]() , m >0
, m >0 ![]() , find value of remaining trigonometric functions?
, find value of remaining trigonometric functions?
(b) Prove that sin100 sin300 sin50° sin70° = .
9. (a) Prove that in an equilateral triangle r: R: r1: r2 : r3 =1: 2: 3 : 3 : 3.
(b) Prove that sin-1 A + sin-1 B = sin-1 (A + B ).