(a) eax ʄ (x)+ c
(b) ![]() eax f (x)+ c
eax f (x)+ c
(c) ![]() f (x)+ c
f (x)+ c
(d) ![]() eax + c
eax + c
FAISALABAD BOARD 2013
PAPER MATHEMATICS
PART-II
Time: 30 Min.
(Objective Part)
Marks: 20
Note: you have four choice for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.
(a) eax ʄ (x)+ c
(b)eax f (x)+ c
(c)f (x)+ c
(d)eax + c
(a)
(x) dx
(b)(x) dx
(c)(x) dx +
(x) dx
(d)(x) dx -
(x) dx
(a) y = cx
(b) y = ce-x
(c) y = e-x
(d) y =cex
(a) Coordinate axes
(b) Radii
(c) Medians
(d) Altitudes
(a)
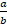
(b)
(c) -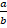
(d)
(a) An equation
(b) Non-inequality
(c) Identity
(d) Inequality
(a) Parabola
(b) Hyperbola
(c) Unit circle
(d) Point circle
(a) a
(b) 2a
(c) 1
(d) 2
(a)
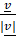
(b)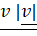
(c)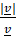
(d)
(a) 1
(b) -1
(c) 0
(d) ab
(a) Linear function
(b) Identity function
(c) Constant function
(d) Non-linear function
(a) 0
(b) 1
(c)
(d) ∞
(a)
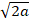
(b)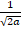
(c)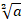
(d)
(a)
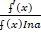
(b)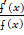
(c) ƒ(x)
(d)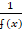
(a) -sin
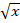
(b)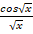
(c)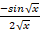
(d)
(a) 0
(b) +ve
(c) -ve
(d) ∞
(a)

(b)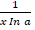
(c)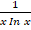
(d)
(a) Derivative
(b) Integral
(c) Differential coefficient
(d) Area
(a) ln |1 + x2| + c
(b) (1 + x2)2 + c
(c) |Tan-1 x | + c
(d) Tan-1 x + c
(a)
sec 3nx + c
(b) n tan nx +c
(c) tan nx + c
(d)tan nx + c
Time: 3:10 Hours
(Subjective Part)
Marks: 83
Section-II
2. Attempt any EIGHT short questions. (8 x2 = 16)
3. Attempt any EIGHT short questions. (8 x2 16)
4. Attempt any SIX short questions. (6 x2 =12)
Attempt any THREE questions. (8 x 3 = 14)
5. (a) If f( x) = 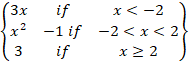 Discuss continuity at x = 2 and x = -2.
Discuss continuity at x = 2 and x = -2.
(b) Differentiate ab -initio with respect to x, y = sin ![]() .
.
6. (a) Show that ƒ ![]() = In (x +
= In (x + ![]() + c.
+ c.
(b) Find the equation of the line through (5,-8) and perpendicular to the join of A(-15,-8) , B (10,7).
7. (a) Solve the differential equation ![]() =
= ![]() ,
, ![]() where x > 0, y > 0.
where x > 0, y > 0.
(b) Maximize f(x, y) = 2x +5y subject to constraints 2y – x ![]() 8, x -y
8, x -y ![]() 4, x
4, x ![]() 0, y
0, y ![]() 0.
0.
8. (a) Find equation of a passing through the points A (-7, 7), B (5, -1), C (10,0)
(b) If ![]() = 3
= 3![]() -
- ![]() - 4
- 4![]() ,
, ![]() = 2
= 2![]() - 4
- 4![]() - 3
- 3![]() and
and ![]() =
= ![]() + 2
+ 2![]() –
– ![]() find a unit vector parallel to 3
find a unit vector parallel to 3![]() - 2
- 2![]() +4
+4![]() .
.
9. (a) Find an equation of the parabola with focus F(1, 2) and vertex (3, 2).
(b) Find the volume of the tetrahedron with vertices (0, 1, 2), (1, 2, 1) and (5, 5, 6)