Federal Board 2013
Statistics Part 1
Note :Circle the correct option.

• 1) The data which have NOT undergone any statistical treatment are ……
  
  a) Primary data
  b) Secondary data
  c) Discrete data
  d) Qualitative data
  
  
• An Ogive is a …………..
  
  a) Frequency curve
  b) Frequency polygon
  c) Cumulative frequency polygon
  d) Frequency histogram
  
  
• The process of arranging data into rows and columns is called ……………1
  
  a) Frequency distribution
  b) Classification
  c) Tabulation
  d) Array
  
  
• Histogram is a graph of ……..
  
  a) Frequency distribution
  b) Time series
  c) Qualitative data
  d) Ogive
  
  
• When a distribution is symmetrical and has one mode, the highest point on the curve is called the
  
  a) Mode
  b) Median
  c) Mean
  d) All of these
  
  
• Sum of squares of deviations of the values is least when deviation is taken from
  
  a) Median
  b) Mode
  c) Mean
  d) Harmonic mean
  
  
• The geometric mean of 'a' and 'b' is
  
  a) ab
  b) (a + b)²
  c)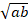
  d)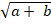
  
  
• Mode of the series 2, 2, 2, 3, 3, 3, 2, 3, 3, 4 is………
  
  a) 3
  b) 5
  c) 8
  d) 1
  
  
• If any value in a series is zero, then we cannot calculate the …………
  
  a) Mean
  b) Geometric mean  
  c) Mode
  d) Median
  
  
• The positive square root of the variance of a distribution is known as ……
  
  a) Standard deviation
  b) Mean deviation
  c) Absolute deviation 
  d) None of these
  
  
• If x = 5, then which of the following expressions is minimum?
  
  a) Σ (x - 25)²
  b) Σ (x - 5)
  c) Σ | x - 5| 
  d) Σ |x — 25|
  
  
• Standard deviation of 2, 2, 2, 2 and 2 is equal to
  
  a) 2 
  b) 8
  c) Zero 
  d) 4
  
  
• If the moment Ratio ẞ2  = 3 then the distribution is
  
  a) Platykurtic
  b) Positively skewed
  c) Symmetrical
  d) Mesokurtic
  
  
• The price used in the construction of consumer price index numbers is ……
  
  a) The retail price
  b) The wholesale price
  c) The fix price
  d) None of these
  
  
• Base year weighted index numbers are also known as
  
  a) Laspeyre's
  b) Paasche's
  c) Fisher's
  d) None
  
  
• Long term variation is regarded as
  
  a) Secular trend
  b) Seasonal variation
  c) Cyclical variation
  d) Irregular variation
  
  
• The graph of a time series is called a
  
  a) Histogram
  b) Historigram
  c) Trend line
  d) Scatter diagram

Section-II

2. Attempt any Fourteen parts. 42

• Give three examples of Discrete variable.
• Define Frequency distribution.
  
• Describe the empirical relation between Mean, Median and Mode.
  
• The mean of three groups each containing 15 values is 10, 20 and 30. Find mean for all forty-five values.
  
• Find two numbers whose arithmetic mean is 5.0 and geometric mean is 4.0.
  
• Define Arithmetic mean, Geometric mean and Harmonic mean.
  
• Define Semi interquantile range, Mean deviation and Standard deviation.
  
• A student calculated mean and standard deviation of 25 values as 20 and 4, respectively.Find the value of coefficient of Variation.
• If .x: -5.2, 4.4, 3.1 Find its Variance.
• Write three properties of Variance.
• If Paasche’s index number is 105.72 and Laspeyre's index number is 107.22. Find Fisher's index number.
• Distinguish between the Fixed base method and Chain base method used in the construction of index number.
• Find the regression coefficient y on x and the regression coefficient x on y from the following data:
  n = 10, ΣD_x = -8. ΣD_y = 0, ΣD_x² = 66, Σ D_y² = 99 and ΣD_xD_y  =  72
• Define the two regression coefficients.
• Find the correlation coefficient from the regression coefficients:
  a) 1.2 and 0.6
  b) -0.76 and -0.82
• Given n = 100, Σx = 5000, Σ y = 6000,
  Σxy  = 300300, Σx²= 250400 and  Σ y²= 360900
  Calculate the correlation coefficient `r'
• Define Correlation coefficient.
• Define Irregular movements.
• Define Time series and Historigram.

Section-II
Attempt any Two questions. 26

Question#3
a) Find Q3 and Mode for the following data:

b) Calculate Variance and Mean deviation (from mean) for the following frequent distribution:

Question#4
Calculate Laspeyres', Paasches' and Fisher Ideal price index number for the data given below, taking 1946 as base year:

Question#5
a) Fit two lines y = a + bx and x = c +dy by method of least square to the following data:

b) Compute seven-day movin6 averages for the following record of attendance: