Federal Board 2013 Statistics
Part 2
Statistics 
2013

1. Circle the correct option. (17)

•  Neither tail nor head comes up on the upper side of the coin, is an example of ……... set.

• If three six-faced dice are rolled, the possible outcomes are  …………..

• If P(A)    =  P (B) =     , B is a complementary event of event A.

• If E( X ) = 10, a = 2 and h= 5 then E(ax-b) =

• Median of the Binomial distribution      will b  

a)        
b)        
c) 5        
d) 10

• For a symmetrical binomial distribution p and q are

• In normal distribution the 4th mean moment about mean is equal to ……………

 a) 13σ⁴   
b) 3σ⁴      
c) 13σ²          
d) None

• If a normal distribution σ = 10, then M.D. will approximately be……. 

•  S.E. of X for without replacement sampling is …………….

•  Population proportion is a ………..

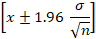•  is the confidence interval for μ; when the level of confidence is... ..
  
  a) 80%             
  b) 90%             
  c) 95%            
  d) 99%
•  Rejecting H₀ , when H₀  is actually false is a ……….

a) Type-I error
b) Type-II error
c) Wrong decision
d) Correct decision

• For a = 0.05, the critical value of Z for two tailed test is …………..

a) ± 2.33
b) ± 1.96
c) ± 2.58
d) None

• Which test-statistic should be preferred to test the population mean when the population variance is known?

a) t-statistic                
b) z-statistic
c) x² – statistic            
d) None

• The calculated value of the Chi-square could NOT be

• If a contingency table consists of four rows and three columns, the d.f will be

• Chi-square distribution is a …………… distribution.

2. Attempt any Fourteen parts  (42)

•  Show that in a single throw with two dice. The probability of throwing more than 7 is equal to that of throwing less than 7.
• Find the probability that on a single draw from a pack of playing cards, we draw a Diamond card or Picture card Or Both.
•  Write down the properties of Mathematical Expectation.
• If for ʄ(x) = 6 – 7 |7 – x| for x : 2,3,4,5,6,12,36
  find the variance of the random variable "X".
• What is Binomial Distribution and what are its properties?
• A random variable x is binomially distributed with mean 3 and variance 2. Compute P(x = 6)
• If X is a binomial random-variable with n = 5 and P = 0.6 then find
  E(2 X - 3) and Var (2 X -3)
• Write down the properties of the Normal distribution.
• The two quartiles of the normal distribution are 9 and 18, respectively. Find the Mean and Standard deviation of the distribution.
• Define Standardized Normal Variate. Also write equation of the normal curve for standardized normal variate.
• Differentiate between Probability and Non-probability Sampling.
• What is the value of the finite population correction factor (f.p.c),
  when n= 18 and N = 125
• Differentiate between Point-estimate and Interval- estimate.
• Given n= 500,  = 0.08, Z0.005 = 2.58.
  Find the 99% Confidence Interval for the population  proportion.
• Describe the difference between One-sided and Two-sided tests.
• Given H0 : μ1 – μ2  = 0 vs H1 : μ1 – μ2  ≠ 0
  When n1 = 11, n2 = 14 , x1 = 75, x2 = 60
  (n1 – 1)S12 = 372.1, (n2 – 1) S22 = 365.34
  Find the value of "t" - Statistic.
• What is the difference between Simple and Composite Hypothesis?
  
• Given the following information
  (a)= 54 , (aẞ) = 16, (B) = 490 and = 1000
  Show whether attributes A and B are positively-associated. negatively-associated or independent.
  
• What is meant by Association of attributes?

Attempt any Two questions.

 3. a) A random variable X has the probability distribution

 Find:

• The value of K.
• P( X < 0 ) and P (X > -1)

3. b) A finite population consists of numbers 2, 2. 4. 6 and 5, written on 5 tags of different colours. Draw all possible random samples of size 2 without replacement from this population and find their means. Construct the sampling distribution of the sample mean and verify that:

• μ = μ     
  
• σ x2 =   

 4. a) If X - N( 30,31.36 ), then find:

         1) P(X > 20)       2)         P(X  25)

 4. b) In a test given to two groups of students, the marks obtained are given below:

Test the hypothesis that  μ1 = μ2 at 5% level of significance, assuming that σ12  = σ22

5. a) A sample of 120 observations from a population known to be non-normal yielded the Sample Values,
X = 576 , S2 = 2475
Find an approximate 90% Confidence Interval for mean of the population.

5. b) The following table shows the distribution of 200 school children according to their Physical defect  and Speech defect. Use a= 0.01

Do the data suggest any association between Physical defect and Speech defect?