Inter (Part-I)
Gujranwala Board 2013
Mathematics
Paper: I
Time: 30 Minutes
Marks: 20
OBJECTIVE
Note: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct, fill that circle in front of that question number with marker or pen on the answer book provided. Cutting or filling two or more circles will
result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank.
-
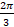 radians equals:
radians equals:
(A)120°
(B) 150°
(C) 270°
(D) 190°
- cos
 equals:
equals:
(A) 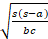
(B) 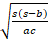
(C)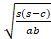
(D) 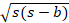
- Solution of 1 + cosx = 0 which lies in [0 , 2 π] is:
(A) 0
(B) π
(C) 
(D) 2 π
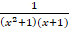 =
= 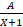 +……..
+……..
(A) 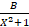
(B) 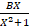
(C) 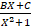
(D) 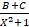
(A) 9!
(B) 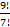
(C) 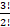
(D) 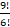
- If n is even then, (a + x)n has:
(A) two middle terms
(B) no middle term
(C) one middle term
(D)  middle terms
middle terms
- Period of sin
 function is:
function is:
(A) 2π
(B) 
(C) 10π
(D) 5π
- The matrix obtained by interchanging its rows and columns is called:
(A) inverse
(B) transpose
(C) symmetric
(D) adjoint
- If 2 and 3 are roots of a quadratic equation, then equation is:
(A) x2 + 5x - 6 = 0
(B) x2- 5x + 6 = 0
(C) x2- 5x - 6 = 0
(D) x2 + 5x + 6 = 0
- The circum-radius R is given as:
(A) 
(B) 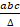
(C) 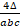
(D) 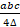
- cos(
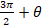 ) equals:
) equals:
(A) cos θ
(B) -cos θ
(C) - sin θ
(D) sin θ
- Domain of the function y = sin-1 x is:
(A) 0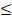 x
x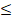 1
1
(B) -1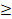 x
x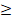 1
1
(C) -1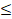 x
x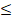 1
1
(D) -1<x<1
- Next term of the sequence 1,3,7,15,31,…. is:
(A) 63
(B) 62
(C) 80
(D) 81
(A) n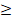 3
3
(B) n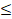 3
3
(C) n<3
(D) n>3
- For two numbers a and b, G2 equals:
(A) A.H
(B) A - H
(C) A + H
(D) 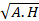
- {1 , -1} is closed with respect to:
(A) addition
(B) multiplication
(C) division
(D) subtraction
- If AB exists, then (AB)-1 is:
(A) A-1B-1
(B) (BA)-1
(C) B-1A-1
(D) AB
- If P(E) is a probability of an event E, then:
(A) 0<P(E)<1
(B) 0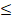 P (E)
P (E)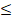 1
1
(C) 0 > P (E) > 1
(D) 0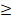 P (E)
P (E) 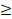 1
1
- Converse of p
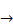 q is:
q is:
(A) 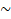 p
p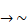 q
q
(B) p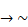 q
q
(C) q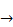 p
p
(D) 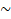 q
q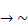 p
p
- If the roots of px2 + qx + 1 = 0 are equal, then:
(A) p2 + 4q = 0
(B) p2 - 4q = 0
(C) q2 + 4p = 0
(D) q2 - 4p = 0
Inter (Part-I)
Gujranwala Board 2013
Mathematics
Paper: I
Time: 2.30 Hours
Marks: 80
SUBJECTIVE
Note: Section I is compulsory. Attempt any Three (3) questions from Section II.
(Section -I)
2. Write short answers to any EIGHT questions: (2x8 = 16)
- Define the terms: rational number and irrational number.
- Does the set {0, -1} possess closure property w.r.t. addition and multiplication?
- Write down power set of {a, (b , c) }.
- Check whether p
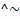 p is a tautology or not.
p is a tautology or not.
- What are row matrix and column matrix?
- Find adjoint and
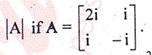
- If A is symmetric matrix, show that A2 is symmetric.
- Without expansion show that
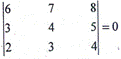
- Solve x (x + 7) = (2x - 1) (x + 4) by factorization.
- If α , β are roots of 3x2 - 2x + 4 = 0, find value of
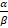 +
+ .
.
- Show that sum of all cube roots of unity is zero.
- Evaluate (1 +
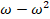 ) (1-
) (1-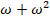 )
)
3. Write short answers to any. EIGHT questions: (2x8 = 16)
- Define partial fraction.
- Resolve
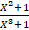 into partial fractions with unknown constants.
into partial fractions with unknown constants.
- If
 ,
, ,
, are in A.P, then show that b=
are in A.P, then show that b=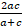 .
.
- How many terms of the series - 9 - 6 - 3 + 0 + …..amount to 66?
- Convert the recurring decimal 2.33 into an equivalent common fraction.
- If 5 is harmonic mean between 2 and b, find b.
- How many signals can be given by 5 flags of different colours using 3 flags at a time?
- Find n if nC12 = nC6.
- How many arrangements. of the letters of word `PAKISTAN' taken all together can be made?
- A die is rolled. What is the probability that the dots on the top are greater than 4?
- Calculate (2.02)4 by binomial theorem.
- If x is so small that its square and higher power can be neglected, then show that
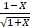 = 1-
= 1- x.
x.
4. Write short answers to any NINE questions: (2x9 = 18)
- If cot θ =
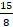 and the terminal arm of the angle is not in first quadrant, find the values of cos θ and cosec θ.
and the terminal arm of the angle is not in first quadrant, find the values of cos θ and cosec θ.
- Prove that
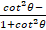 = 2 cos2 θ-1.
= 2 cos2 θ-1.
- Prove that sin (α +β) sin (α - β) = cos2 β- cos2 α .
- Prove that cos (α + 45°) =
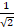 (cos α - sin α).
(cos α - sin α).
- Prove that cot a - tan a = 2cot 2a.
- Prove that
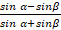 = tan
= tan 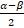 cot
cot 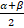 .
.
- Find the period of tan
 .
.
- A vertical pole is 8 m high and the length of its shadow is 6 m. What is the angle of elevation of the sun at that moment?
- Measure of two sides of a triangle is in the ratio 3:2 and they include an angle of measure 57°. Find the remaining two angles.
- Solve the triangle ABC in which a = 32 ; b = 40 : c = 66
- Prove that r r1 r2 r3 = ∆2
- Find the solution of cosec θ = 2 which lie in [0 , 2π ].
- Find the solution set of the equation: tan 2θ+ cot θ = 0 .
(Section -II)
5.a) Show that the set {1, ω, ω2} is an abelian group with respect to multiplication. 5
b) Solve by Cramer’s rule
3x1+x2-x3=-4
x1+x2-2x3=-4
-x1+2x2-x3=1
6.a) Solve the equation x6-9x3+8=0
b) Resolve 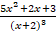 into partial fractions. 5
into partial fractions. 5
7. a) If  ,
, ,
, are in G.P, show that the common ratio is
are in G.P, show that the common ratio is 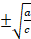 . 5
. 5
b) Find the term involving x-2 in the expansion of 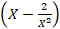 13.
13.
8.a) Find trigonometric ratios of 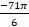 . 5
. 5
b) Prove that cos 20° cos40° cos60° cos80° = 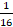 5
5
9.a) Solve triangle ABC, given that α = 35° , 17' β=40°, 13' b = 421 . 5
b) Prove that sin-1 A + sin-1B = sin-1 (A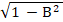 +B
+B 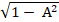 ). 5
). 5
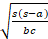
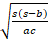
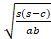
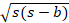

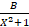
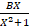
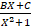
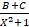
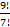
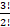
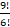
middle terms


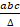
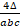
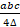
x
1
x
1
x
1
3
3
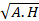
P (E)
1
P (E)
1
p
q
q
p
q
p
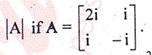
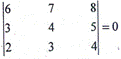
![]() into partial fractions. 5
into partial fractions. 5![]() ,
,![]() ,
,![]() are in G.P, show that the common ratio is
are in G.P, show that the common ratio is ![]() . 5
. 5 ![]() 13.
13. ![]() . 5
. 5![]() 5
5![]() +B
+B ![]() ). 5
). 5