(A) in-centre
(B) centroid
(C) e-centre
(D) circumcentre
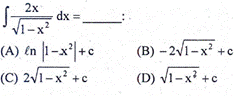
Inter (Part-II)
Gujranwala Board 2013
Mathematics
Paper: II
Time: 30 Minutes
Marks: 20
OBJECTIVE
Note: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct, fill that circle in front of that question number with marker or pen on the answer book provided. Cutting or filling two or more' circles Will
result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank.
(A) - 4
(B) 4
(C) 28
(D) 0
(A) Vertex of the parabola
(B) Axis of the parabola
(C) Latus-rectum of the parabola
(D) Focal chord of the parabola
(A) Feasible region
(B) Optimal solution
(C) Convex region
(D) Feasible solution set
(A) in-centre
(B) centroid
(C) e-centre
(D) circumcentre
(A) 1 sq unit
(B) 2 sq unit
(C) 3 sq unit
(D) 4 sq unit
(A)
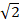
(B)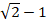
(C)+1
(D) 1
(A) ax
(B) ax . ℓn a
(C)
(D)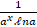
(A)
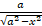
(B)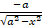
(C)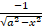
(D)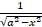
(A) 1
(B) cosh 2x
(C) sinh 2x
(D) 2cosh 2x
(A) y = cosec x + c
(B) y = sec x + c
(C) y = - cosec x + c
(D) y = -cot x + c
(A) 0
(B) 1
(C) 2
(D) 10
(A) 1
(B) 8
(C) 4
(D) 16
(A) c
(B) a
(C) b
(D) 0
(A) x = a sin θ
(B) x = a sec θ
(C) x = a cos θ
(D) x = sin θ
(A) 2, -2
(B) 2, 6
(C) 4. -4
(D) 4, 2
(A)
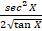
(B)sec2x
(C)
x. sec2 x
(D)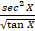
(A) 0
(B) 1
(C) sin x
(D) cos x
(A)

(B)log a.
(C)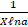
(D)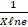
(A) 0
(B) 1
(C) -1
(D) 2
Inter (Part-II)
Gujranwala Board 2013
Mathematics
Paper: II
Time: 2.30 Hours
Marks: 80
SUBJECTIVE
Note: Section I is compulsory. Attempt any three (3) questions from Section II.
(Section - I)
2. Write short answers to any EIGHT questions: (2x8 = 16)
3. Write short answers to any EIGHT questions: (2x8 = 16)
4. Write short answers to any NINE questions: (2x9 = 18)
(Section - II)
5.a) Evaluate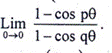 (5)
(5)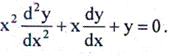 (5)
(5)6.a) Show that ![]() =ℓn
=ℓn![]() (5)
(5)
b) Find h such that the points A(![]() ,-1), B(0,2) and C (h, -2) are the vertices of a right triangle with right angle at the vertex A. (5)
,-1), B(0,2) and C (h, -2) are the vertices of a right triangle with right angle at the vertex A. (5)
7.a) Evaluate ![]() x+
x+![]() dx. (5)
dx. (5)
b) Graph the feasible region and find the corner points of linear inequalities 2x - 3y ![]() 6, 2x + 3y < 12, x 0, y>0. (5)
6, 2x + 3y < 12, x 0, y>0. (5)
8.a) Find an equation of a circle passing through A(-3 , 1) with radius 2 and centre at 2x - 3y + 3 = 0. (5)
b) If a = 3i - j - 4k ,b= -2i -4j-3k,c=i+2j-k Find a unit vector parallel to 3a - 2b + 4c. (5)
9.a) Find focus, vertex and directrix of the parabola x2 - 4x - 3y + 13 = 0. (5)
b) Prove by vector method that cos (α -β) = cos α cosβ + sin a sigβ. (5)