Gujranwala Board»
(Inter Part —II 2013)
Subject: Statistics (Obj. Type)
Total Marks: 17
Time  Allowed: 20 Min.
Note:- You have four choices for each objective type question as A, B, C and D. The choice which you think is correct, fill that circle in front of that question number with marker or pen on the answer book provided Cutting or filling two or more circles will result in zero mark in that question (Attempt as many questions paper given in objective type question paper and leave other blanks.

Question#1

• A computer device that can capture images Is called
  
  (A) monitor
  (B) plotter
  (C) Scanner
  (D) C.P.U.
  
  
• The graph of time series is called
  
  (A) Straight line
  (B) Ogive
  (C) Histogram
  (D) Histogram
  
  
• When A and B have perfect positive association, then
  
  (A) Q=+1
  (B) Q=-1
  (C) Q = 0
  (D) Q= 0.99
  
  
• If bxy, = —1 and byx = —1, then r is equal to
  
  (A) +1
  (B) -1
  (C) 0
  (D) 0.5
  
  
• An alternative hypothesis is also called
  
  (A) True hypothesis
  (B) Null hypothesis
  (C) False hypothesis
  (D) Research hypothesis
  
  
• E(ⱺ) —ⱺ is called
  
  (A) Sampling error
  (B) Non sampling error
  (C) Standard error
  (D) Bias
  
  
• The errors caused during processing information are called
  
  (A) Sampling errors
  (B) Non sampling errors
  (C) Standard errors
  (D) Bias
  
  
• The parameters of the r normal distribution are
  (A) µ
  (B) µ and C5
  (C) µ and Q.D
  (D) M.D.
  
• Normal distribution is a limiting form of
  
  (A) Hyper geometric distribution
  (B) F-distribution
  (C) Binomial distribution
  (D) X2-distribution
  
  
• Separating the four components for study is called
  
  (A) time series
  (B) analysis of time series
  (C) residual series
  (D) geometric series
  
  11. A table consisting of r rows and c columns is called r x
  
  (A) Frequency table
  (B) T-table
  (C) F-table
  (D) Contingency table
  
  
• The formula of r is given by
  
  (A)  
  (B)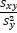
  (C)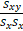   
  (D)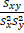  
  
  
• The degrees of freedom for a -test for paired observations “are
  
  (A) n
  (B) n-1
  (C) (r — 1) (c — 1)
  (D) n1 + n2 — 2
  
  
• The variable whose value is predicted is called
  
  (A) Independent variable
  (B) Random variable
  (C) Regressand
  (D) Regressor
  
  
• The population about which some information is required is called
  
  (A) Finite population
  (B) Infinite population
  (C) Target population
  (D) Smpled population
  
  
• The simple random sampling is
  
  (A) Non probability sampling
  (B) Probability sampling
  (C) Systematic sampling
  (D) Quota sampling
  
  
• The range of the normal distribution is
  
  (A) 0 to ∞
  (B) 0 to n
  (C) - ∞ to + ∞
  (D) - ∞ to 0

Gujranwala Board
(Inter Part — II) 2013
Subject: Statistics (Sub. Type)
Paper - II
Total Marks: 68
Time Allowed: 2:40 hrs.
Section-I
Note:- Section I is compulsory.attempt any three (3) questions from Section II.
(SECTION-I)

• Define standard normal variate.
  
• If X - N (100,100), find the value of maximum ordinate of normal curve.
  
• If u = 85, ⱺ = 4.5, find the value of Q3 of normal distribution.
  
• Write any two properties of normal distribution.
  
• If X - N (100, 64), find the value of
  (i) M.D. (ii) Q.D.
  
• Distinguish between   
  (i) estimate (ii) estimator,
  
• What is meant by unbiasedness?
  
• Define statistical inference.
  
• Distinguish between
  (i) null hypothesis (ii) alternative hypothesis.
  
•   Define region of rejection.
  
• Explain that C.P.U. is brain of computer.
  
• Distinguish between RAM and ROM.

3. Write short answers to any EIGHT questions:

• Write any two advantages of sampling.
  
• Differentiate between random sampling and non-random sampling.
  
• Define sample design.
  
• Enlist the various methods of selecting the simple random samples.
  
• Define sampling distribution.
  
• All possible samples are drawn from a normal population with mean = 50 and
  S.D. = 5. What is the sample size if the
  S.E. of Xis 1.0?
  
• Explain the principle of least squares.
  
• What is a scatter diagram?
  
• Write the relationship  between regression coefficients and correlation coefficients.
  
• Interpret the meanings of when r = + 1 and r + —1.
  
• If rxy = —0.75, Sy = 5 and ∑(x — x)(y —y) = —15n, then find Sx
  
• Write down the two formulas of correlation coefficient by direct method and indirect method.

4. Write short answers to any SIX questions:    

• Explain the term secular trend.
  
• What is meant by cyclical variation?
  
• Give two examples of seasonal variation.
  
• Define the method of moving average.
  
• What is time series?
  
• Given y = 1, 2, 3, 4,  x = 0,  1, 2
  
• If y= 0.6 +1.2 x, find ,∑(y —y
  
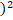
• Are A and B independent if (AB) = 12
  
• (A) = 30 (B) = 40 N = 100
  
• What is negatively association?
  
• What are the properties of rank correlation coefficients?

(SECTION-II)

Question#5

(a) In a normal distribution, mean and variance are 20 and 25 respectively. Find P( x > 22) and P(22 < x < 28).
(b) The scores made by candidates in a test are normally distributed with mean 500 and standard deviation 100.
What percentage of candidates received scores?
(i) Between 400 and 600
(ii) Less than 400

Question#6
(a) A population contains 2, 4, 6 values. Take all possible samples of size 2 with Replacement from this population. Construct sampling distribution of sample means and sample  variances. Find mean of distributions.
(b) Suppose 60% of city population favours public finding for a proposed facility. If 150 persons are to be randomly selected and interviewed, what is the mean and standard error of sample proportion favouring this issue?

Question#7
(a) Find point and 95 % confidence interval estimates separately for 4 taking following sample: 50, 70, 90, 110, 130, 150, 170, 190, 210 and 230.Assuming ⱺ2 is unknown and population is normal.
(b) Test the hypothesis Hᵒ : µ < 10 against suitable alternative hypothesis using a = 10%, ⱺ = 5 and following sample values: 8, 12, 15, 6, 7, 12, 11, 15 and 9.

Question#8
(a) Compute three coefficients with reference to correlation and regression from the following information:
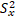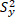∑(x - x)(y –y)  = 150, = 64, = 260
and n = 16
(b) Develop regression equation to estimate time (t) if speed (s) is provided using following set of   'observations:

Question#9
(a) There are 240 A's and 270 B's in 600 observations. What would be the number of AB's if A and B are independent? 4
(b) Fit a straight line from the following information for the year 1995 to 2000 (both inclusive)
∑x = 0,  ∑y = 264, ∑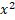 = 70, ∑xy = 30. Find out the trend values as well.