(A) ![]()
(B)![]()
(C) ![]()
(D) 0
Inter (Part-I)
Lahore Board 2013
Mathematics (New Scheme)
Time Allowed: 30 Minutes
OBJECTIVE
Max. Marks: 20
Note: Four possible answers A, B, C and D to each question are given. The choice which you think is correct, fill that circle in front of that question with Marker or Pen ink. Cutting or filling two or more circles will result in zero mark in that question.
(A) 4
(B) 6
(C) 7
(D) 8
(A)
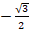
(B)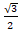
(C)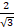
(D) 0
(A) cos
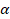
(B) cos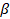
(C) cos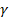
(D) sin
(A)
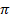
(B) 2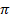
(C) 3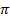
(D) None of these
(A) 8
(B) 4
(C) -4
(D) -8
(A) 45°
(B) 90°
(D) 360°
(C) 270°
(A)

(B)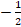
(C) 2
(D) -2
(A)
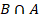
(B)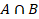
(C)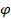
(D)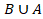
(A) Two middle terms
(B) 3 middle terms
(C) 4 middle terms
(D) 0 middle term
(A) 360°
(B) 335°
(C) 270°
(D) 225°
(A) x + 1
(B) x-1
(C) x - 3
(D) x + 5
(A) 3
(B)2
(C) 4
(D) 6
(A)
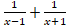
(B)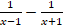
(C)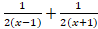
(D)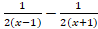
(A)
(B) –
(C)
(D)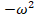
(A) [-1,1]
(B) [-1,1)
(C)[0,π]
(D)[0,π)
(A) Circumcircle
(B) In-circle
(C) E-circle
(D) Semicircle
(A) {2nπ}
(B) {π +2nπ}
(C) {π}
(D) {2π +nπ}
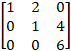 is
is (A) Diagonal
(B) Scalar
(C) triangular
(D) Singular
(A)
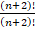
(B)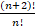
(C)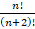
(D) (n+2)!
(A) (-1,0)
(B) (0,-1)
(C) (0,1)
(D) (1,0)
Inter (Part-I)
Lahore Board 2013
Mathematics
Time: 2.30. Hours
Paper: I
Marks: 80
SUBJECTIVE
(Section - I)
2. Write short answers to any EIGHT (8) questions: (16)
3. Write short answers to any EIGHT (8) questions: (16)
4. Write short answers to any NINE (9) questions: (18)
Section (II)
Attempt any THREE questions
5. a) Show that the set {1,![]() } when
} when ![]() is an abelian group w.r.t. ordinary multiplication
is an abelian group w.r.t. ordinary multiplication
b) Find inverse of the matrix, A=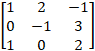
6. a) Show that (1+![]() ) (
) (![]() ) (
) (![]() ) (
) (![]() )---- 2n-factor =1 where
)---- 2n-factor =1 where ![]() is cube root of unity
is cube root of unity
b) Resolve into partial fractions![]()
7.a) Find n so that ![]() may be H.M between a and b
may be H.M between a and b
b) If y =![]() -------then prove that
-------then prove that ![]()
8.a) If cos![]() , find value of remaining trigonometric functions?
, find value of remaining trigonometric functions?
b) Prove that sin 10osin 30osin 50osin 70o =![]()
9.a) Prove that in an equilateral triangle r:R:r1:r2=1:2:3:3:3
b) prove that sin-1 A+sin-1 B=sin-1![]()