INTERMEDIATE PART-I (11Ih CLASS)
STATISTICS PAPER-I
TIME ALLOWED:20Minutes
OBJECTIVE
MAXIMUM MARKS: 17
Note: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct, fill that circle in front of that question number, Use marker or pen to fill the circles. Cutting or filling two ur more circle will result will be zero mark in that question.
Attempt is many questions as given in onjective type question paper and leave other blank. No credit will be awarded In case 'BUBBLES arc not filled, Do not solve question on this sheet of OBJECTIVE PAPER.

Question#1

• The norms cure is:
  
  (A) Leptokurtic
  (B) Mesokurtic
  (C) Platykurtic
  (D) Skewed
  
  
• The area outside the range of x= (μ ± σ) of normal curve is approximately equal to:
  
  (A) 0.16
  (B) 0.05
  (C) 0.32
  (D) 1
  
  
• In normal distribution, 1 and 2  respectively are
  
  (A) 3 and 0
  (B) 3 and 3
  (C) 0 and 3
  (D) 0 and 0
  
  
• Quota sampling belongs to:-
  
  (A) Probability sampling
  (B) Random sampling
  (C) Non-random sampling
  (D) Systematic sampling
  
  
• Survey conducted through sampling design is called:-
  
  (A) Population survey
  (B) Sample survey
  (C) Census
  (D) National survey
  
  
• The difference between estimated and actual values of parameter a called;-
  
  (A) Standard Error
  (B) Sampling Error
  (C) Non-sampling Ergot
  (D) None of these
  
  
• If is an estimator of Q,  then . 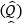is cilled unbiased if:-
  (A) E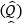>Q
  (B) E<Q
  (B) E=Q 
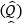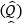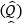  (D) E≠Q
  
• A teacher passed a bad student is an example of:-
  
  (A) Type-1 Error 
  (B) Typc-11 Error
  (C) Right Decision
  (D) Sampling Error
  
  
• What would be the alternative hypothesis against the null hypothesis o ?
  
  (A) μ < μ₀
  (B) μ > μ₀
  (C) μ ≥ μ₀
  (D) μ ≠ μ₀
  
  
• The possible range of r is:-
  
  (A) 0 to 1
  (B) -1 to 0
  (C) -1 to +1
  (D) -∞ to +∞
  
  
• r is equal to:.
  
  (A)
  (B)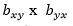   
  (C)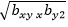
  (D)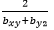
  
  
• In regression equation y 10 = 2x , slope of the line is:-
  
  (A) 10
  (B) -2
  (C) 2
  (D) Unknown
  
  
• The degree of freedom for testing independence of two attributes through chi-square is:- 
  
  (A) r x c
  (B) r x (c-1)
  (C)(r-1) x c
  (D) (r —1)(c — 1)
  
  
• always:-
  
  (A) Least
  (B) Maximum
  (C) Negative
  (D) Unknown
  
  
• Increaie in demand of ice in summer is an example oft-
  
  (A) Souniar Trend
  (B) Seasonal Variation
  (C) Cyclical Variation
  (D).Riindons
  
  
• The fo Unit 6,encration computers veorked on:-
  
  (A) VacEnuri Tube
  (B) Oil Transistors
  (C) Integrated Circuit
  (D) Aieroprocessor

INTERMEDIATE PART-II
(STATISTICS)
PAPER-II
TIME ALLOWED: 2.40 Hours 
SUBJECIVE
MAXIMUM MARKS: 68
NOTE: Write same question number and part number in answer book, given in the question paper
SECTION-1

• What is Standard Normal  distribution?
  
• What are the Mean and Variance of the Normal Distribution?
  
• Write short  note on the Normal Distribution.
  
• Write the Lower and Upper quartile  of  Normal Distribution.
  
• Explain why β1 = 0 for the Normal Distribution. 
  
• Difine type II error with example.
  
• Differentiate between point Estimated and Point Esimated.
  
• Distinguish between One- sided and Two sided Test. 
  
• Define  statically Hypotheses.
  
• Define ∝           .
  
• What is RAM in the Computer
  
• What are the Output devices in the Computer?

3. Attempt any eight parts. 16

• Differentiate between  Sample Random Sampling and Stratified Random Sampling.
  
• Given N = 7,   n = 2 and = 16.If sampling is done without replacement then End E( S2 ).
  
• Explain the Sampling without replacement
  
• De rile the Sampling Distribution of Means.
  
• Define the Non-sampling Error.
  
• Differentiate between Finite and Infinite population.
  
• Given  ∑ (x -x ) (y - y )²= 0  ,∑ (x -x)²= 10,  ∑ (y - y)²  = 10 and n = 5 Find the Co-efficient of correlation.
  
• Differentiate between, Regression and Correlation.
  
• Given  = 72,   = 4  and   = 18,  Find the value of  
  
• Given  = 5,   = 4,   ∑y = 100,   ∑ xy = 484  and ∑ y2 = 425.Determine the regression co-efficient of x on y
  
• What is meant by correlation co-efficien and write prorerties.
  
• Given  b_xy = -1.4     and     r_xy = -0.87.Find b_y

4. Attempt any six parts. 12

• Define Time series.
  
• Define Secular Trand with ex amples.
  
• Given 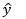 =128 + r 4x and  x = -3, - 2, -1, 0, 1,  2,  3 Find ∑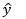
  
• Define Semi Average Method
  
• What is Forecasting?
  
• What are the Components of the series?
  
• Define  x² chi- square distribution.
  
• What do you understand by association?
  
• Define Variables and Attributes with examples.

SECTION-II

NOTE:Attempt any three questions.
Question#5
(a) In a normal distribution mean is 20 and standard deviation is 5 Find mean deviation and quartile deviation.
(b) In a normal Distribution μ = 24,&²= 16 then find
(i) 33^rd percentile
(ii) 9th decile

Question#6
(a) A population consists- of values 2 4, 6, 8 . Draw all posible samples of size n = 2 with replacement from the population and show that:  =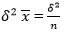
(b) Given the following population Distribution :

Find δ when n = 4 with replacement
Find δ  when n = 2 without replacement.
Is the proporion of even numbers in the sample.

Question#7
(a) Find 95% confidence interval for  μ  from the sample of size 8 with value 7. 9, 10, 11,  12, 13, 14.
(b) A firm of light bulbs claims that average life time of its products is 3500 hours. A random sample of 15 bulbs is taken and found that average life time is 3450 hours
And SD = 200 hours. Test Ho : μ < 3500 at α = 5%

Question#8
(a) For the following paired data (x, y)  find the estimated Line of regression of y on x . (0, 1),(1,1,8)    (2, 1,3 ), (3, 2,5) (4, 6, 3) Also show that ∑ (y -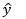) = 0
(b) Given the following result :    r.0.5,     ∑ (x -x) = 90, ∑ (x -x )(y -y= 120 &) S_y = 8 then compute the number of items i,e. n=?

Question#9
(a) Find rank correlation co-efficient from the following  data:-

(b)    The 2nd degree parabola for the years from 1992 to 1999 is = 472 – 21  X – 2X² with origin at the middle of 1995 arid 1996 and unit of measurement  X is one year. Compute trend values for 1992 to 1999.