s
Untitled Document
RAWALPINDI BOARD 2013
PAPER MATHEMATICS
PART-I
Time: 20 Min.
(Objective Part)
Marks: 17
Note: You have four choice for each objective type question as A,B,C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.
- If b2 - 4ac < 0 in quadratic equation ax' + bx + c = 0, then roots are:
(a) Rational
(b) Equal
(c) Real and unequal
(d) Complex / imaginary
- Partial fraction be of tlic torts:
(a)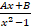
(b)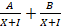
(c)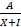
(d)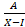
- If an (-1)n+1 then 26th term of the sequence is:
(a) 1
(b) -1
(c) 26
(d) 2
- In the infinite geometric series, "S" equals to:
(a) 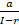
(b) 
(c) 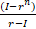
(d)  {2a + (n-I)d}
{2a + (n-I)d}
 belongs to set of:
belongs to set of:
(a) Real numbers
(b) Complex numbers
(c) Prime numbers
(d) Even numbers
- The domain of f ={(a,1),(b,1),(c,1)} is:
(a) {a.b,c}
(b) {a}
(c){I}
(d){b,c}
- If A=
 , then |A| is equal to:
, then |A| is equal to:
(a) 46
(b) -46
(c) 38
(d) -38
- If all the entries of a row (or a column) of a square matrix arc zero then |A|is equal to:
(a) 1
(b) 2
(c) 3
(d) 0
- If α,β are the roots of the equation x2 - 4x + 5 = 0, then aft is equal to:
(a) 5
(b) -4
(c) 2
(d) 4
- Radius of escribed circle opposite to vertex A is:
(a) 
(b) 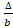
(c) 
- In the triangle ABC the law of tangent is:
(a) 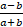 =
= 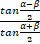
(b)  =
= 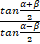
(c) 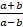 =
= 
(d) 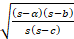
- Range of cos x is equal to:
(a) [-1,1]
(b) 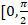
(c) [1,100]
(d) [-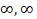
- If sins =
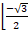 , then solution is:
, then solution is:
(a) 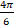 ,
, 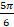
(b) 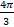 ,
, 
(c) 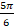 ,
, 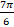
(d)  ,
, 
- The value of
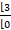 is equal to:
is equal to:
(a) 0
(b) ∞
(c) 3
(d) 6
- If
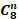 =
=  then n is equal to:
then n is equal to:
(a) 0
(b) 8
(c) 20
(d) 12
- The sum of odd coefficients in the binomial expansion of (1- x) is:
(a) 2n-1
(b) 2n+1
(c) 2n
(d) 2n -1
- If n is positive integer, then n! > n2 is true when:
(a) n 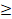 4
4
(b) n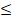 4
4
(c) n <4
(d) n= 2
- If tan θ> 0, sin θ <0, the terminal arm of angle lies in:
(a) I quadrant
(b) 11 quadrant
(c) Ill quadrant
(d) IV quadrant
(a) 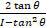
(b) 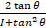
(c) 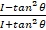
(d) 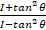
- Period of sin
 is:
is:
(a) π
(b) 3π
(c) 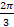
(d) 6π
Time: 3:10 Hours
(Subjective Part)
Marks: 83
Section-I
2. Attempt any EIGHT short questions. (8 x 2 = 16)
- Find the multiplicative inverse of (-4,7).
- If Z
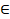 C. show that Z
C. show that Z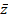 - =|z|2
- =|z|2
- Construct truth table for (p
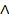
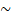 p)
p)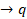
- Define the Rank of a matrix.
- Find three cube roots of unity.
- Solve x2 + 6x -567 = 0 by completing squares.
- If 'A' is non-singular matrix, then show that (4-1) =A
- If a,
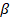 are roots of ax2 + bx +c= 0 then find the value of a2+
are roots of ax2 + bx +c= 0 then find the value of a2+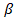 2.
2.
- When x4 +2x3 – kx2 +3 is divided by (x-2) the remainder is ‘I’. Find the value of K.
- If A= [
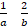 ] and A2[
] and A2[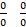 ]then fin ‘a’ and ‘b’.
]then fin ‘a’ and ‘b’.
- Without expansion verify that
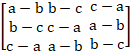 -0
-0
- Find the inverse function relation {(x ,y)/y =2x +3}+.
3. Attempt any EIGHT short questions. (8 x 2 = 16)
- What is conditional equation ?
- Define proper rational fraction
- Find A.M between
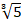 and ,
and ,
- Find the II`" term of sequence 1 + i , 2,
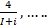
- If a =
 andb=
andb= find A and G.
find A and G.
- Find the value of n , if
- Define the term "permutation".
- State the principle of Mathematical Induction .
- Check whether
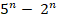 is divisible by 3 for n =1,2.
is divisible by 3 for n =1,2.
- How many signals can be given by 5 flags of different colours , using 3 flags at a time
- 4 dice is thrown twice , what is the probability that sum of the number of dots shown is 3 or 11?
- If
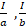 and
and  are in A.P , show that the common difference is
are in A.P , show that the common difference is 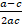
4. Attempt any NINE short questions. (6 x 2 = 12)
- Convert 30° to Radians
- Flow many minutes are in two right angles?
- Show that tan (45+A) tan (45-A) =1.
- Show that cos(147°) = cos(33°).
- Proves that sin 60 cos 30 -cos 60 sin 30 =

- Show that sin =
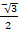
- What is the domain of tan x?
- What is right angle trangle?
- What is hypotenuse of right angle tringle?
- Solve cot2 a =

- Find solution cos ecx=2an [‘0,2
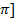
- Find unknown angles and sides of right angle tringle with y= 90° ,
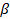 = 50°,10'c = 0.832
= 50°,10'c = 0.832
Attempt any THREE questions. (8 x 3 = 24)
5. (a) Let a = the set of all english alphabets A= {x / x is vowel},B= {y /y is consonant). Verify DeMorgan's Laws for these sets.
(b) Show that:  =I2(3a+I)
=I2(3a+I)
6. (a) If 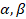 be the roots of 5x2 –x - 2 = 0, then form the equation whose roots are
be the roots of 5x2 –x - 2 = 0, then form the equation whose roots are  and
and .
.
(b) Resolve into partial fraction : 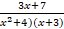
7. (a) Find 11th term o f G.P + I, ,……….
,……….
(b) Find term independent of x in the expansion of (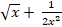 )10
)10
8. (a) Find the values of the trignontetric functions, if sin θ= -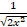 and terminal arm is not in the III quadrant.
and terminal arm is not in the III quadrant.
(b) Prove that: cos3a = 4cos3 a - 3 cos a.
9. (a) The sides of a triangle are x2 + x + 1, 2x + 1 and x2 - I Prove that the greatest angle of the triangle is 120°.
(b) Prove that: tan-1 tan-i  tan-1
tan-1 = tan-1
= tan-1 
![]()
![]()
![]()
![]()
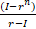
{2a + (n-I)d}

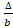

=
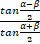
=
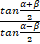
=

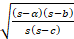
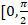
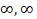
,
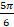
,

,
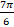
,

4
4
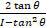
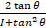
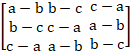 -0
-0 =I2(3a+I)
=I2(3a+I)![]() be the roots of 5x2 –x - 2 = 0, then form the equation whose roots are
be the roots of 5x2 –x - 2 = 0, then form the equation whose roots are ![]() and
and![]() .
. ![]()
![]() ,……….
,……….![]() )10
)10![]() and terminal arm is not in the III quadrant.
and terminal arm is not in the III quadrant.![]() tan-1
tan-1![]() = tan-1
= tan-1 ![]()