RAWALPINDI·BOARJJ 2013
PAPER MATHEMATICS
PARt-II
Time:30Min.
(Objective Part)
Marks:20
Note: You have four choice for each objective type question as A,B,C and D. The choice which you think is correct ; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or fill in two or circles will result in zero mark in that question.
(a)

(b)
(c)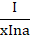
(d)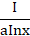
(a) -1
(b) 0
(c) 1
(d) 2
(a) In |x sin x| +c
(b) In |x sin2 x| +c
(c) In|ex cos2 x| +c
(d) In |xcos2 x| +c
(a) tan-1
+c
(b) cot-1+c
(c) sin-1+c
(d) In |x ++ c
(a) 4x +1
(b) 4x+3
(c) 4x – 3
(d) 4x -1
(a) 1 nx
(b) 1 na
(c) 1
(d) 0
(a)
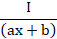
(b)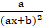
(c)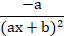
(d) In(ax+b)
(a) Product rule
(b) Power rule
(c) Chain rule
(d) Quotient rule
( a) cos
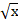
(b)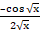
(c)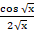
(d)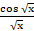
(a) c = 0
(b) c = 1
(c) c = -1
(d) c = f + g
(a) Upward
(b) Downward
(c) Right side
(d) Left side
(a) u vsinθ
(b) v x u
(c) u vcosθ
(d) –v x u
(a) u . v x w
(b)( u . v x w)
(c)( u . v x w)
(d)( u . v x w)
(a)

(b)
(c)
(d) π
(a) -1
(b) -2
(c) 1
(d) 2
(a) e-x cos x +c
(b) e-x sinx +c
(c) ex sinx +c
(d) ex cosx +c
(a) xy =c
(b) In=c
(c) X+y =c
(d)=c
(a) y =mx +c
(b)=1
(c) y-y1 =m (x – x1)
(d) x cosa +ysin a=p
(a) Centroid
(b) Orthocentre
(c) Circumcentre
(d) Incentre
(a) 2
(b) 3
(c) 1
(d) 0
Time : 3:10 Hours
(Subjective Part)
Marks: 83
Section –II
2. Attempt any EIGHT Short Question. (8x2=16)
3. Attempt any EIGHT short question. (8x2 = 16)
4. Attempt any SIX short question. (6 x 2 = 12)
Attempt any THREE question.
5.(a) Evaluate ![]()
(b) If x= a (![]() +sin
+sin![]() and y=(1+cos
and y=(1+cos![]() show that
show that ![]() +a = 0
+a = 0
6. (a) Evaluate ![]() .
.
(b) Find the point which is equidistant from the points A(5,3), B(2,2) and C(4,2). What is the radius of the circum circle of the triangle ABC?
7.(a) ![]() - dθ.
- dθ.
(b) Maximize f(x,y) = 2x +5y subject to the constraints 2y-x![]()
8.(a) Find a unit vector parallet to 3a – 2b +4c if a = 3![]() -
- ![]() -4
-4![]() b = 2
b = 2![]() - 4
- 4![]() + 3
+ 3![]() , c =
, c = ![]() +2
+2![]() 2
2![]() .
.
(b) Find an equation of the circle passing through A(-3,-1) , B(0,1) and having centre at 4x -3y -3 =0.
9.(a) Find an equation of parabola having focus F(-3,1), directrix x = 3
(b) Prove that in a triangle ABC, c2 = a2 +b2 2bc cos C.