Statistics Part - II
Rawalpindi 2013
Marks = 17
Note:Encircle the right option.

• The choice of one and two tailed test depends on
  
  (A) H_a
  (B) H₁
  (C) H₅
  (D) H_-1
  
  
• The d.f. for unpaired samples in T-test with n₁=11 and n₂=10 are
  
  (A) 19
  (B) 21
  (C) 22 
  (D) 20
  
  
• When bxy is positive, then bxy will be
  
  (A) Negative
  (B) Positive
  (C) Fixed
  (D) None
  
  
• The dependent variable is also called
  
  (A) Regressand
  (B) Regressor
  (C) Explanatory
  (D) Fixed
  
  
• For uncorrelated variable the correlation coefficient is
  
  (A) 19
  (B) 21
  (C) 22
  (D) Zero
  
  
• For r x c contingency table. the number of degrees of freedom are
  
  (A) rc
  (B) r+c
  (C) (r-1)+(c-1)
  (D) (r-1)(c-1)
  
  
• The x2 - Test should not be used if any expected equency is
  
  (A) Less than 10
  (B) More than 10
  (C) Less than 5
  (D) More than 5
  
  
• If straight line is fitted to the time series then
  
  (A) ∑(y - yˆ)² =0
  (B) ∑(y + yˆ)² =0
  (C) ∑(- yˆ)² =0
  (D) ∑(y)² =0
  
  
• A time series has components
  
  (A) 19
  (B) 21
  (C) 22 
  (D) 4
  
  
• Keyboard, mouse and scanner are
  
  (A) Head ware
  (B) output devices
  (C) Software
  (D) Input devices
  
  
• The parameters of normal distribution are
  
  (A) 19
  (B) 21
  (C) 22
  (D) 2
  
  
• In normal distribution β1 is
  
  (A) 0
  (B) 1
  (C) 2
  (D) 3
  
  
• The limits including 50% area under normal curve are
  
  (A)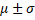
  (B)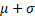
  (C)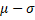
  (D)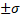
  
  
• In sampling with replacement 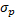 a is equal to
  
  (A)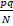    
  (B)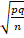    
  (C)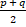
  (D)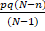 
  
  
• All possible samples of size 4 with replacement from a population of size 2 are
  
  (A) 0
  (B) 16
  (C) 2
  (D) 3
  
  
• Sampling error can be reduced by
  
  (A) Biased
  (B) properly
  (C) Unbiased
  (D) Increasing sample
  
  
• If E(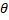)< 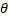, then  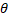d will be
  
  (A) Biased
  (B) Positively biased
  (C) Unbiased
  (D) Negatively biased

 2.Answer any eight parts. 16

• Write y = f(x) of normal distribution for
  (A) Mean = μ and Variance = 2
  (B) Mean = 0 and Variance =1
• Draw Standard normal curve properly indicating Z-values: -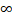, -3, -2, -1, 0, +1, +2, +3, +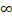
• What are first four moments about mean of the normal distribution? if β1 = 0 and β2 = 3.
• Note the area under the normal curve in ranges:
  (A) Mean ±2(S(D)
  (B) Mean -I- 3( S(D)
• Find three quartiles of the normal distribution having mean 100 and variance 25.
• Write down formulae of two estimators of population standard deviation.
• Describe low-level and high level languages.
• Make difference between point and interval estimation.
• What is critical region in testing of hypothesis?
• Explain in short terms the memory and storage of computer.
• When an estimator is unbiased?
• Define critical value.

3 Answer any eight parts. 16

• Given ∑(X - X)² =175, ∑(y - y)² =142
  ∑(X - X) (Y - Y)= 96. Find b_xy and b_yx
• Write down any two formulae of correlation coefficient.
• Write any two properties of correlation coefficient.
• Define causation in correlation.
• Differentiate between Parameter and Statistic.
• Define population and sample.
• Define sampling distribution.
• What is meant by probability sampling?
• What is without replacement sampling?
• What is sampling error?
• What is intercept and slope?
• Define regression with examples.

4. Answer any six parts. 12

• Given ∑X = 0, ∑Y = 84 ∑XY = 210
  ∑X² = 70 and n =7 Find the values of intercept and slope.
• Given Yˆ = 250 -10X and X = -3,-2,-1,0,1,2,3 Find ∑Yˆ =1750.
• If Y = 2,5,6,8,9 X =1,2,3,4,5 and Yˆ = 0.9 +1.7X .Compute the sum of squares of residuals.
• Find co-efficient of association"Q", if N=800, ((A)=300, (A(B)=270 and ((B)=100
• Discuss the meaning and .purpose of moving averages.
• Differentiate between positive & negative association.
• If ((A)=240. ((B)=270 and N=600. What would be the number of (A(B)? if A and B are independent.
• Explain the method of least squares in time series.
• What is meant by business cycle?

Answer any three questions. 24

Question#5
(A) If X ˜ N(24,16), write down its probability density function. Find the ordinate of its normal curve at X=21. Also find its maximum ordinate.
(B) In a normal distribution Q₁=10 and Q₃=22. Find mean and standard deviation of the distribution.

Question#6
(A) A population consists of four values 2, 4. 5 and 6. Draw all possible samples of size two with replacement. Find the proportion of even numbers in each sample. Construct the sampling distribution of sample proportion of even numbers and verify that
(i) μP = p 
(ii)  =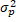
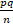
(B) Given N₁=800, N₂=600, n₁=200, n₂=124, μ₁ = 1800, μ₂ =1600 , 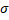1 = 200, 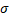2 =124. Compute the mean and standard error of the sampling distribution of the Difference (X₁ - X₂), if sampling is done.
(i) with replacement
(ii) without replacement

Question#7
(A) Find a 95% confidence interval for P1-P2 if: n₁=10, n₂=20, X₁=6, X₂=8.
(B) Given a sample of 10 values: 10, 7, 11, 15, 10, 12, 9, 16, 12, 10. Test H₀: μ = 10 against H_1:μ>10 .Use 5% level of significance.
Question#8
(A) Find byx and bxy, from the following information:
∑(X - 17) = 2, ∑(X - 17)² =218
∑(Y - 15) =48, ∑(Y - 15)² =1366
∑(X - 17) (Y - 15) =464, n = 30
(B) Find the r from the data given below.

Question#9
(A) During influenza epidemic 15 boys and 8 girls became ill out of a class of 32 boys and 38 girls.
(i) Draw up a 2 x 2 contingency table.
(ii) Formulate the null and alternative hypothesis to test
the independence of sex and influenza.
(B) For the following time series data compute the trend values by fitting a straight line.