SAHIWAL BOARD 2013
PAPER MATHEMATICS
PART-I
TIME : 20 MIN.
(OBJECTIVE PART)
MARKS: 17
NOTE: YOU HAVE FOUR CHOICES FOR EACH OBJECTIVE TYPE QUESTION AS A,B,C and D. THE CHOICE THAT YOU THINK IS CORRECT ; FILL THAT CIRCLE IN FRONT OF THAT QUESTION NUMBER. USE MARKER OR PEN TO FILL THE CIRCLES. CUTTING OR FILLING TWO OR MORE CIRCLES WILL RESULT IN ZERO MARK IN THAT QUESTION.
- Polar form of complex number. X +iy is.
(a)r cosθ + r sinθ
(b)rcosθ + irsinθ
(c)cosθ +sinθ
(d)sinθ +icosθ
- If A= {a,b,c,d} then number of elements in its power set are.
(a)16
(b)4
(c)8
(d)12
- If order of matrices A and B is m x n then order of A x B is.
(a)m+n
(b)m-n
(c)m x n
(d)m÷n
- A square matrix “A” is said to be symmetric if A’ =
(a)A
(b)-A
(c)A-1
(d)A2
- Three cube roots of 27 are:
(a)3,ω,ω2
(b)-3,-3ω,3ω2
(c)3,3ω,3ω2
(d)1,ω,ω2
- Roots of equation ax2 + bx +c = 0 are real and equal if:
(a)b2-4ac=0
(b) b2-4ac>0
(c) b2-4ac<0
(d)4ac-b2>0
- A fraction in which the degree of the numerator is less then the degree of the denominator is called:
(a)proper fraction
(b)improper fraction
(c)equation
(d)in – equation
(a)a1 + nd
(b)a1 + (n-1)
(c)a1 +n/d
(d)a1 d+n
- A.M between
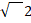 and
and 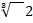 is :
is :
(a)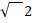
(b)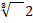
(c)2
(d)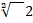
(a)1
(b)n!
(c)n!/ (n-r)!
(d)(n-1)!
- If AпB = Ø then P (AUB) = :
(a)P(A) +P(B)
(B)P(A) – P(B)
(C)P(A) P(B)
(D)P(A)+P(B)-P(AпB)
- IF “n” is nay positive integer then 4n > 33 +4 is true for all:
(a)n>2
(b)n≥2
(c)n<2
(d)n≤2
- The expansion of (1+ 2x)-1 is valid only if:
(a)x<2
(b)x>2
(c)x<1/2
(d)x>1/2
- If sinθ > 0 and cot θ > 0 then in which quadrant the terminal arm of angle “θ” lies:
(a) 1-quad
(b) 2-quad
(c) 3-quad
(d) 4-quad
(a)tan θ
(b)- tanθ
(c)cot θ
(d)-cot θ
(a)R
(b)[-1,1]
(c)R-nπ
(d)R -2nπ
- In right triangle no angle is greater then:
(a)45°
(b)30°
(c)80°
(d)90°
(a)abc/4Δ
(b)Δ/s
(c)s/Δ
(d)Δ
(a)π/6
(b)1/2
(c)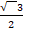
(d)1
- The general solution of the equation 1 + cos x = 0 is :
(a){π/2 + 2nπ}
(b){-π/2 + 2nπ}
(c){π + 2nπ}
(d){π + nπ}
TIME : 3:10 HOURS
(SUBJECTIVE PART)
MARKS : 83
SECTION II
2. ATTEMPT ANY EIGHT SHORT QUESTIONS. (8 x 2 = 16)
- Find the multiplicative inverse of (1,0).
- Simplify i(101).
- Verify de morgan’s law for the sets U = {1,2,3………..,20},A= {2,4,6,……,20}, B= {1,3,5,………19}.
- Construct truth table for the statement (p→~p) v (p→q)
- Define unit matrix.
- If A =
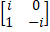 , show that A4 = I2
, show that A4 = I2
- Find the inverse of
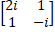
- Verify that
(AB)’ = B’.A’ if A=
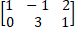 B=
B= 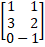
- Solve x2/5 + 8 = 6x1/5.
- Find the three cube roots of 8.
- Find the condition that root of x2 +px +q=0 is double the other.
- The sum of a positive number and its square is 380. Find the number.
3. attempt any eight short questions. (8 x 2 = 16)
- Resolve into partial fractions 3x/ (x-1)(x+2).
- Change x4/1-4x4 into proper fraction.
- If 1/a, 1/b ,1/c are A.P show that b = 2ac/a+c
- If Sn = n(2n-1) , then find the series.
- Find 9th term of H.P , -1/5, -1/3 -1,…………
- How many words can be made from the letters of PAKISTAN.
- FIND N , WHEN C5 = C4.
- Find the numbers of diagonals of a 6 sided figure.
- If P2 = 30, find n.
- Verify the statement, 1+3+5+……….+2(2n-1) = n2 for n = 3.
- Expand (2 – 3x)2 upto four terms.
4. Attempt any six short questions. (6 x 2 = 12)
- Find angle and its directions.
- Convert 21.256° to the degree, minute, second from.
- Prove that sin (a-β).sin(a +β) = sin2 a – sin2 β.
- Show that sin 2 θ = 2 tan θ/(1 + tan2 θ).
- Express cos (2x +30°). Cos (2x - 30°) as sums or differences.
- Prove that sin 3a = 3sin a – 4sin3 a.
- Prove that tangent is a periodic function and its period is π.
- Prove that sin r/2 =
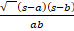
- Find the area of the triangle ABC, given two sides and internal angle, a = 4.33, b = 9.25, y = 56° 44’
- Show that r = (s-a) tan a/2
- Prove that r1 r2 r3 = rs2.
- Solve the equation 4 cos2 x-3 =0 in [0,2π].
- Solve the equation 1 + cos x = 0.
Attempt any three questions. (8 x 3 = 24)
5.(a) Show that the statement is a tautology . ~(p→q) → p.
(b) Verify (AB)-1 = B-1 A-1 , if A= 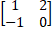 B =
B = 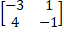
6.(a) Solve the equation (x – 1/x)2 3(x +1/x) = 0
(b) Resolve into partial fractions x2/ (x2+ 4) (x+ 2)
7.(a) Find “n” so that an + bn/an-1 + bn-1
(b) Use mathematical induction to prove the formulae for every positive integer n 1+ ½ + ¼ +……………. 1/ 2n-1 = 2 [1-1/2n]
8.(a) Prove the following identity sin6 θ +cos6 θ = 1 -3sin2 θcos2 θ
(b) If a,β,y are angles of a triangle ABC show that.Cot a/2 + cot β/2 + cot y/2 = cot a/2 cot β/2 cot y/2
9.(a) Prove the law of
(b) Find the value of cos-1 4/5 without using calculator.
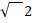
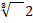
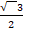
![]() B =
B = ![]()