SAHIWAL BOARD 2013
PAPER MATHEMATICS
PART-II
TIME ALLOWED: 30 Minute
(Objective Part)
MAXIMUM MARKS: 20
Note: You have four choices for each objective type question as A, B, C and D .The choice which you think is correct, fill that circle in front of that question number. Use marker Or pen to fill the circle. Cutting or filling two or more circles will result in zero mark in that question.
a.

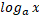
b.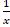
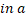
c.
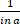
d.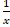

a.
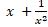
b.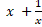
c.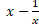
d.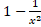
a.
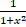
b.
c.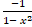
d.
a.1
b.-1
c.0
d.x
a.cosec2ax
b. a cosec2ax
c. -a cosec2ax
d.
a.even function
b.identity function
c.odd function
d.linear function
a.circle
b.parabola
c.hyperbola
d.ellipse
a.
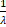
+c
b.
+c
c.+c
d.+c
a.
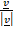
b.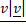
c.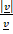
d.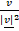
a.1
b.-1
c.0
d.ab
a.linear function
b.identify function
c.constant function
d.non linear function
a.0
b.1
c.1/2
d.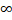
a.
+c
b.+
+ c
c.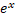
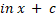
d.-
+ c
a. 2:3
b. 2:5
c. 1:2
d. 3:5
a.1
b.2
c.0
d.n
a.parameters
b.constants
c.decision variables
d.vertices
a.
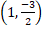
b.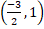
c.(1,-2)
d.(1,2)
a.(
)
b.(0,)
c.()
d.(0,)
a.vector product
b.cross product in three vectors
c.inner product
d.none of these
a. scalar product
b. vector product
c. cross product
d. meaningless
(Subjective Part)
TIME ALLOWED: 3:10 Hours
MAXIMUM MARKS: 83
SECTION II
3. Attempt any eight short questions. (8x2=16)
4. Attempt any SIX short questions. (6 x 2 = 12)
Attempt any THREE questions. (8 x 3 = 24)
5 .(a![]() )=
)=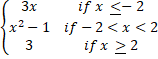 Discuss the continuity of f(x) at x =2 and x = -2
Discuss the continuity of f(x) at x =2 and x = -2
(b) If x = sinθ and y = sin mθ ,show that (1-x2)y2-xy1+m2y =0.
6.(a) Evaluate ![]()
(b) Find the conditions that the lines y=m1x+c1;y=m2x+c2;y=m3x+c3 are concurrent.
7. (a) Evaluate the definite integral ![]() 2 dx.
2 dx.
(b) Graph the feasible region subject to the following constraints:2x-3y ![]() 6; 2x+y
6; 2x+y ![]() 2;x
2;x ![]() 0; y
0; y ![]() 0.
0.
8. (a) Find equations of the tangents to the circle x2+y2 =2.Perpendicular to the line 3x + 2y = 6.
(b) Prove that the line segment joining the mid points of two sides of a triangle is parallel to the third side an half as long.
9.(a) Find the focus, vertex and directrix of the parabola y=6x2-1.
(b) Find the volume of tetrahedron with vertices (0,1,2),(3,2,1),(1,2,1) and (5,5,6).