Mathematics
(Objective)
Maximum Marks:- 20
Time Allowed:- 30 minutes
Note:-You have four choices for each objective type question as A, B, C and D. The choice which you think is covert; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filing two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave other blank. Use of ink remover or white correcting fluid is not allowed.
Q. 1
(A) 5
(B) -5
(C) 25
(D) -25
(A) Empty set
(B) Non empty net
(C) Proper set
(D) Improper set
(A) 1
(B) 2
(C) 3
(D) 4
(A) (0,0,1)
(B) (0,1,0)
(C) (1,0 0)
(D) (0,0,0)
(A) a=0
(B) a≠0
(C) b=0
(D) b≠0
(A) f(-a)
(B) f(-1/a)
(C) f(1/a)
(D) f(a)
(A) Proper fraction
(B) Improper fraction
(C) Common fraction
(D) Irrational fraction
(A) 40
(B) 42
(C) 44
(D) -42
(A)
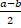
(B)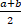
(C)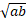
(D)
(A) 5
(B) 10
(C) 15
(D) 20
(A)
(B) 1/6
(C) 2
(D) 1/3
(A)
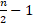
(B)
(C)
(D)
(A) n>1
(B) n≥1
(C) n=1
(D) n≥4
(A)
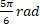
(B)
(C)
(D)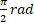
(A)
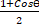
(B)
(C)
(D)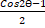
(A) -∞<y< ∞
(B) -∞<y< 0
(C) -∞ ≤ y ≤ ∞
(D) 0<y<2π
(A) R
(B) r
(C) r1
(D) r2
(A) b2+c2=a2
(B) c2+a2=b2
(C) a2+b2=c2
(D) b2- c2 =b2
(A) Sin-1A+Sin-1B
(B) Sin-1A – Sin-1B
(C) Cos-1A+Cos-1B
(D) Cos-1A-Cos-1B
(A) x/3, 2x/3
(B) x/4, 3x/4
(C) 5x/3, 4x/3
(D) 1x/6, 5x/6
Mathematics
(Subjective)
Time Allowed: 2.30 hours
2. Answer briefly any Eight parts from the followings:
3. Answer briefly any eight parts from the followings:- (8 x 2 = 16)
4. Answer briefly any Nine parts from the followings: (9 x 2 = 18)
Section----ll
Attempt any three questions. (10 x 3 = 30)
5-(a) Show that the set {1,ω,ω2}when ω3=1 is an Abelian group w.r.t ordinary multiplication.
(b) Using Cramer's Rule solve system of equations
2x + 2y + z=3
3x - 2y - 2z =1
5x + y - 3z= 2
6-(a) Show that the roots of x2+(mx+c)2=a2will be equal, if c2=a2 (1+m2)
(b) Resolve ![]() in to Partial fractions
in to Partial fractions
7-(a) Find the vulgar fraction of 1.53
(b) Find 6th term in the expansion of (![]() )10
)10
8-(a) Prove the result:![]() =
=![]()
(b) If α+β+ϒ = 180°, show that Cotα Cotβ + Cotβ Cotϒ+ Cotϒ Cotα=1
9-(a) Prove that r r1 r2 r3=∆2
(b) Prove that Sin-1 ![]() + Sin-1
+ Sin-1 ![]() = Sin-1
= Sin-1 ![]()