Inter (Part-II) Bahawalpur Board 2014
Mathematics
Part I (Objective Type)
Time Allowed: 20 Minutes
Max. Marks: 17
Note: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.
Question #1
Circle the correct option i.e. A/B/C/D. Each part carries one mark.
(a) Even
(b) Odd
(c) Both Even and Odd
(d) Neither Even or Odd
(a)
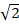
(b) 2
(c)
(d) 0
(a)
(b)
(c)
(d) 3
(a)
(b)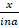
(c)
(d)
(a)
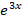
(b)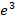
(c)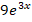
(d)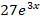
(a) f (c)=0
(b) f(c) > 0
(c) f(c) < 0
(d) f (c) > 0
(a) x-
+
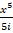
(b) 1-+
+
(c) -x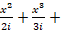
(d) x-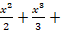
(a) 2x
(b) 2xdx
(c) 2x
(d) 2x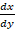
(a)
+c
(b)+c
(c)+c
(d)+c
(a) 5Sin5x+c
(b)sin5x
(c) -5Sin5x+c
(d) -sin5x + c
(a)
+c
(b) inx + c
(c) (inx+c
(d) in(inx) +c
(a) In (ax-1) +c
(b) aln (ax-1)+c
(c)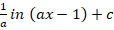
(d)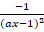
(a) in(xy) = 0
(b) in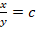
(c) xy = c
(d) in=c
(a)
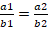
(b)=
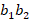
(c)+
=0
(d)= 0
(a) 13
(b)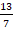
(c)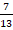
(d)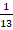
(a) x+y > 0
(b) (6, -4)
(c) (3, -2)
(d) x-y = 0
(a) (-6, 4)
(b) (6,-4)
(c) (3,-2)
(d) (-3, 2)
(a) (a, 0)
(b) (-a,0)
(c) (0,0)
(d) (0, -a)
(a) (
)i+(
)j
(b) ()i+(
)j
(c) ()i+(
)j
(d) ()i+(
)j
(a) -4
(b) 4
(c) 1
(d) 0
Inter (Part-II) Bahawalpur Board 2014
Mathematics
Part II (Subjective)
Time Allowed: 2.30 Hours
Max. Marks: 80
Section I
Q.No.2
Q.No3
Q.No.4
Section-II
Question #5
(a) For the real valued function f, defined below find:
(i) ![]()
(ii)![]() (-1) and verify f
(-1) and verify f![]() (f(x)) = x f(x) = (-x+09)³
(f(x)) = x f(x) = (-x+09)³
(b) If y = aCos (lnx) + bSin(inx), prove that ![]() + x
+ x ![]() +y = 0
+y = 0
Question #6
(a) Evaluate ∫x![]() xdx
xdx
(b) Find the equation of line through the point (2, -9) and the intersection of the lines 2x + 5y -8 = 0 and 3x -4y -6 = 0
Question #7
(a) Evaluate ![]() dx
dx
(b) Maximize (x,y) = 2x+3y subject to the constraints 2x+y < 8
X + 2y < 14, x > 0 , y > 0
Question #8
(a) Find equation of the circle pssing through A (3, -1) B (0, 1) and having centre at 4x-3y -3 =0
(b) Prove that angle in a semi circle is a Right Angle.
Question #9
(a) Show that the equation 9x2 -18x + 4y2 + 8y = 0 represents an ellipse Find in centre foci vertices and co-vertices
(b) Prove that Sin (∞-B) = Sin∞ CosB -Cos∞ SinB by vector method