FAISALABAD BOARD 2014
PAPER MATHEMATICS
PART-I
Time: 30 Min
(Objective Part)
Marks: 21
Note: Four Answers are given against each column A, B, C & D, Select the write answer and only separate answer sheet. fill the circle A,B,C or D with pen or marker in front of that question number.
- A, G, H are arithmetic. Geometric , harmonic means between a and b respectively then A,G,0 are:
(a) In G.P.
(b) In A.P.
(c) In H.P.
(d) All of these
- The next term of the sequence 7,9,12 ... is:
(a) 16
(b) 15
(c) 14
(d) 18
- A relation in which the equality is true for only finite values of unknowns is called an:
(a) Identity
(b) Equation
(c) Trigonometric equation
(d) Algebraic relation
- Four fourth roots of unity are:
(a) -1,1,I,-i
(b) -2,2,-2i,2i
(c) -3,3,3i,-3i
(d) ±4,±4i
- If (x- 2) is a factor of ax2 - 12x + 4 then a =
(a) 2
(b) 5
(c) 7
(d) 9
- If A =
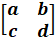 then adj (A) = :
then adj (A) = :
(a) 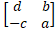
(b) 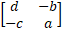
(c) 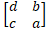
(d) 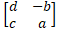
- For any non-singular Matrix A, A-1 is:
(a) |A|adj(A)
(b) 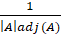
(c) 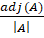
(d) 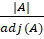
- If every element of a set A is also element of the set B, then:
(a) A  B
B
(b) B ⊆ A
(c) A∩B=Φ
(d) A∩B=AC
(a) Set builder form
(b) Tabular form
(c) Descriptive loan
(d) non-descriptive form
- Golden rule of fraction is that for k ≠0,
 =
=
(a) 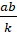
(b)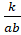
(c)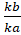
(d)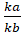
- Solution of 1 + cos x = 0 is:
(a) 
(b) π
(c) 2π
(d) 
- sec(cos-1
 )=
)=
(a) 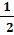
(b) 2
(c) 
(d) 
(a) 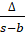
(b) 
(c) 
(d) 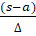
- The period of 3 sin 3x is:
(a) 
(b) 
(c)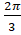
(d) 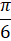
(a) cos (α+β)+ cos (α-β)
(b) cos (α+β) - cos (α-β)
(c) sin (α+β)+ sin (α-β)
(d) sin (α+β) - sin (α-β)
- The 60th part of 1- degree is called one:
(a) Second
(b) Radian
(c) Degree
(d) Minute
- The second term in the expansion of
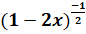 is:
is:
(a) x
(b) 2x
(c) 3x
(d) 4x
- If n is any +ve integer then 12 + 22 + 32+ ………….+ n2=
(a) 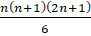
(b)

(d) 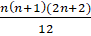
- n-different objects taken all at a time can be arranged in:
(a) (n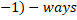 )
)
(b) (n—1)!—ways
(c) n!-ways
(d) (2n)!-ways
(a) n+1Pr
(b) nPr+1
(c) n-1Pr
(d) nPr
Time: 2:30 Hours
(Subjective Part)
Marks: 80
SECTION-I
2. Attempt any Eight Parts.
- Prove that
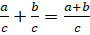
- Separate
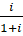 into real and imaginary perts.
into real and imaginary perts.
- Write down the power set of
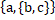
- Show that
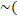 p
p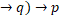 is a tautology.
is a tautology.
- For A={1,2,3,4}, state the domain and range of the relation {(x,y)|y=x} in A.
- Define a group.
- Find the matrix x if x
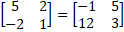
- If A and B are non-singular matrices, then show that (AB)-1 =B-1A-1
- If A is symmetric then show that A2 is symmetric.
- Evaluate (1 + ω-ω2) (1-ω+ω2)
- Find the remainder by remainder theorem when the polynomial x2+3x+ 7 is divided by x + I
- If α,β are the roots of x2- px- p-c =0, then prove that
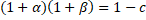
3. Attempt any Eight Parts.
- Define rational fraction.
- If
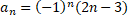 ,find first four terms of the sequence.
,find first four terms of the sequence.
- Fine the number of terms in A.P, in which a1=11, an=68,d=3
- Find the sum of the infinite G.P. 2,
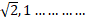
- Find A,G,H (G>0) if a =2 , b =8.
- Find the values of n when nP2= 30.
- Find the value of n when nC10 =

- If s={1, 2, 3, 4, 5}, find the probability of numbers multiple of 3.
- There are 5 green balls and 3 red balls in a box. Find the Probability of one ball taken out is green.
- Prove that 3" < n! For integral values n=7 and 8.
- Find 6th term in the expansion of
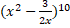
- Find the three terms in the expansion of

4. Attempt any Nine Parts.
- Convert the radian measure of angle into measure of sexagesimal system
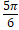
- Verify sin 2θ = 2sinθ cosθ for θ =45°
- If sinθ =
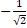 then find the value of cos θ if θ does not lie in the III quadrant.
then find the value of cos θ if θ does not lie in the III quadrant.
- Show that tan (α+β)=
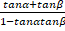
- Prove that sin (45° + α) =
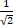 (sin α + cos α)
(sin α + cos α)
- Express the product as sum OR difference 2 Sin >θ sin 2θ.
- Find the period of cos 2x.
- A vertical pole is 8m high and length of its shadow is 6m. What is the angle of elevation of the sun at that moment?
- Solve the triangle ABC in which a=7, b=3,
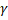 = 38°13
= 38°13
- Prove that R=
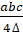
- Evaluate without using table OR calculator cos-1

- Complete the formula tan-1A + tan-1B =
- Solve the equation 1 + Cos x= 0 .
SECTION-II
Attempt any THREE questions. Each question carries equal marks
5. (a) Solve the system of linear equation by Crammer's rule:
2x1 – x2 +x3 = 8
x1+ 2x2, +2x3= 6
x1 - 2x2 - x3 = 1
(b) Solve the equation (x+ I)(x+ 2)(x+ 3)(x + 4) = 24.
6. (a) Resolve into partial fraction.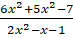
(b) Find vulgar fraction equivalent to the recurring decimal 1.147.
7. (a) A box contains 10 red, 30 white and 20 black marbles. A marble is drawn at random. Find the probability that it is either red or white.
(b) Use mathematical induction to prove that the given formula rule for every positive integer n.
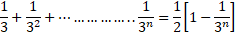
8. (a) Prove that 
(b) Prove that (without using the table/calculator).  .
.
9. (a) Prove that in an equilateral triangle, r:R:r1:r2:r3=1:2:3:3:3
(b) Prove that 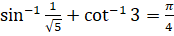
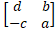
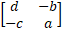
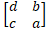
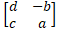
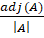
B
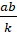
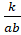
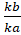

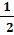

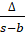




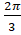
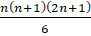
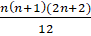
)
![]()
![]()
![]()
![]() .
.![]()