FAISALABAD BOARD 2014
PAPER MATHEMATICS
PART-II
Time: 30 Min
(Objective Part)
Marks: 21
Note: Four Answers are given against each column A, B, C & D, Select the write answer and only separate answer sheet. Fill the circle A,B,C or D with pen or marker in front of that question number.
(A) 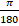
(B) 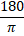
(C) 1
(D) 180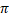
- The value of
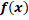 is 2 for all x, then
is 2 for all x, then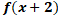 =:
=:
(A) -2
(B) –x+2
(C) 2
(D) x+2
- The notation used by Leibniz for derivative is :
(A) 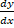
(B) 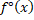
(C) 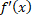
(D) ƒ(x)
- The tangent to a curve us perpendicular to x- axis if:
(A) 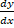 =0
=0
(B) 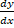 =-1
=-1
(C) 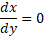
(D) 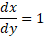
- Differentiating x6 w.r.t. x3, we get:
5x4
3x2
2x2
2x3
(A) 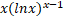
(B) 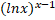
(C) 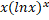
(D) None of these
(A) 2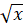
(B) 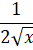
(C) 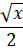
(D) 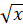
- The area between x-axis and curve y=sin2x form x=0 x=
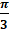 is:
is:
(A) 
(B) 
(C) 0
(D) 1
- If
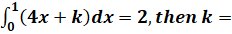 ……………
……………
(A) -1
(B) 0
(C) 1
(D) 2
(A) 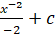
(B) x+c
(C) –x2+c
(D) Lnx
(A) 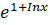
(B) 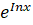 +c
+c
(C) 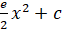
(D) 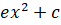
(A) -1
(B) 0
(C) 1
(D) 2
(A) 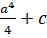
(B) 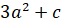
(C) 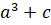
(D) None of these
- The y-intercept of the line 2x+3y-1=0 is:
(A) 
(B) 
(C) 2
(D) 3
- A quadrilateral having two parallel and two non- parallel sides called:
(A) Square
(B) Rectanle
(C) Trapezium
(D) Paralelogram
- x=-1 is in the solution of:
(A) 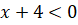
(B) 2x+3 < 0
(C) 3x+4 < 0
(D) X < 0
- The equation of a circle does not contain term involving:
(A) 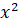
(B) 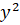
(C) xy
(D) None of these
- Axis of parabola
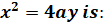
(A) x = 0
(B) y = 0
(C) x = y
(D) x = -y
- The direction consines of a vector parallel to z-axis are:
(A) 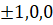
(B) 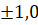
(C) 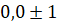
(D) 1,1,1
- 2
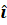 x2
x2 =:
=:
(A) 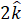
(B) 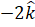
(C) 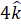
(D) 0
Subjective Part II
Section –I
2. Attempt any Eight parts.
- Find the domain and range of the function
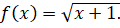
- Evaluate
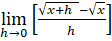
- Find the derivative of the function
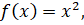 by definition
by definition
- Differentiate
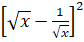 w.r.t ‘x’
w.r.t ‘x’
- Find
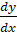 if x=at2 and y=2at
if x=at2 and y=2at
- If y=cos
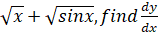
- Find
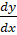 if y=tanh(x2)
if y=tanh(x2)
- If
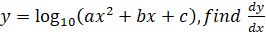
- Find
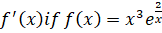 (x≠0)
(x≠0)
- Find y2 if x2+y2=a2
- Prove that
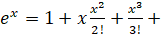 …………
…………
- Define increasing and decreasing function
3. Attempt any Eight parts
- If
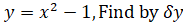 and dy when x changes from 3 to 3.02
and dy when x changes from 3 to 3.02
- Evaluate
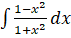
- Evaluate
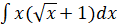
- Evaluate
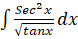
- Evaluate
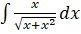
- Evaluate
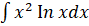
- Evaluate
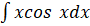
- Evaluate
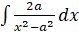
- Evaluate
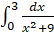
- Solve the differential equation
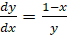
- Graph the solution set of
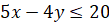
- Define the feasible solution set
4. Attempt any nine parts
- Find the distance between the point. A
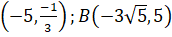
- Transform the equation 4x+7y-2 = 0 in normal form
- Find an equation of the line through (-4,7)parallel to the line 2x-7y+4 = 0
- Find the area of a triangular region whose vertices are A(5,3), B(-2,2), C(4,2)
- Find the point of intersection of the lines x-2y+1 = 0; 2x-y+2 = 0
- Find center and radius of the circle x2+y2-6x+4y+13 = 0
- Write down equation of tangent to the circle x2+y2 = 25 at (4,3).
- Find the focus and vertex of parabola y2 = 8x
- Find the foci, eccentricity of ellipse x2+4y2 = 16
- Write the Vector
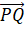 in the form
in the form 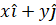 , when P(2,3) Q(6,-2)
, when P(2,3) Q(6,-2)
- Find direction cosines of v=
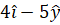 .
.
- Find a scalar α, so that the vectors 2i+aj+4k and3i+j+ak are perpendicular.
- Find the constant α, such that the vectors i-j+k, i-2j+5kand 3i-aj+5k are coplanar.r
Section-II
Note: Attempt any THREE questions. Each questions carries 10 Marks
5. (a) Evaluate 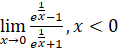
(b) Show that 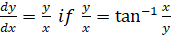
6.(a) Evaluate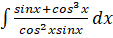
(b) Prove that the linear equation ax+by+c = 0 in two variables x and y represents a straight line.
7.(a) Solve the differential equation 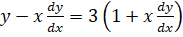
(b) Maximize ƒ(x,y) = 3x+y, subject to the constraints x+6y>9,3x+5y>15,x>0,y>0.
8. (a) Find equation of tangent to circle x2+y2 = 2perpendicular to line 3x+2y=6
(b) Prove that in any triangle ABC, b=c cosA+a cosC (By vectors method)
9. (a) Find an equation of ellipse whose focus is at (±3,0) and minor axis of length 10.
(b) Prove by vector method that sin(α + β) = sin α cos β - cos α sin β
=0
=-1
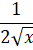
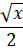


+c
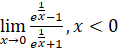
![]()
![]()
![]()