Federal Board 2014
MATHEMATICS
HSSC-I
Time allowed: 25 Minutes
Marks: 20
SECTION — A
NOTE: Section-A is compulsory. All parts of this section are to be answered on the question paper itself. It should be completed in the first 25 minutes and handed over to the Centre Superintendent Deleting/overwriting is not allowe(D) Do not use lead pencil.
Q1. Circle the correct option i.e. A/B/C/(D) Each part carries one mark.
(A) Transitive
(B) Symmetric
(C) Reftexive
(D) Additive
(A) i
(B) -i
(C) -1
(D) 1
(A) A
(B) B
(C) Φ
(D) X
(A) 3x2
(B) 2x2
(C) 3x3
(D) 2x3
(A) >0
(B) <0
(C) =0
(D) Perfect square
(A) 2n+1
(B) 2n+3
(C) 2n-2
(D) 2n - 8
(A) a - b
(B)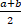
(C) a + b
(D) a x b
(A) n + 1
(B) n-1
(C) n
(D) 2n
(A) 1
(B) 2
(C) 3
(D) 4
(A) 0
(B) 1
(C) 2
(D) None of these
(A) tan 11°
(B) cot 11°
(C) tan 56°
(D) cot 56°
(A) π
(B)
(C) 2π
(D) None of these
(A) 2
(B) 8
(C) ±4
(D) None of these
(A) I
(B) II
(C) III
(D) IV
(A) 1,2,3
(B) A, B, C
(C)
(D) a, b, c
(A) S
(B) s-a
(C) Δ
(D) Δ2
(A)
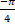
(B) π/2
(C)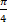
(D) π
(A) x-axis
(B) y-axis
(C) Both A and B
(D) None of these
(A) Root
(B) Element
(C) Index
(D) None of these
(A) n!
(B) n
(C) (n -1)
(D) None of these
MATHEMATICS HSSC-I
Section - B
(Mark 40)
2. Attempt any TEN parts. All parts carry equal marks.
Section - C (Mark 40)
Note: Attempt any FIVE questions. All questions carry equal marks.
Q.3 Simplify (-![]() -
-![]() i)
i)
Q.4 Use matrices to solve 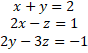
Q.5 If ω is a root of x2 + x + 1 = 0, show that its other root is ω2 and prove that ω2 and prove that ω3 = 1
Q.6 Solve the system of equations
3x + 4y = 25 ,
![]()
Q.7 If 2y = ![]() then prove that 4y2 + 4y - 1 = 0
then prove that 4y2 + 4y - 1 = 0
Q.8 Reduce cos4 θ to an expression involving only function of multiples of θ, raised to the first power.