Federal Board
HSSC-II 2014
MATHEMATICS
Time allowed: 25 Minutes
Marks: 20
NOTE: Section-A is compulsory. All parts of this section are to be answered on the question paper itself. It should be completed in the first 25 minutes and handed over to the Centre Superintendent. Deleting/overwriting is not allowed. Do not use lead pencil.

SECTION — A

Q. 1 Circle the correct option i.e. A / B / C/ D. Each part carries one mark.

• A function of the form f(x,y) = 0 is called                        function.

(A) Parametric      
(B) Implicit
(C) Explicit        
(D) Identity

• (ex) =

(A) ∞
(B) -∞
(C) 0                 
(D) 1

  (A)
(B)
(C)
(D)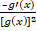

•  is the derivative of

(A) cos^-1 x             
(B) sin^-1 x
(C) cosh^-1 x       
(D) sinh^-1 x

(A) ln|cosx|+ c
(B) ln|secx|+ c
(C) ln|sec2x|+ c
(D) sec2x+ c

(A) Inlcosxl + c
(B) In|secx|+ c
(C) In Isec2xl + c        
(D) sec2x + c

• The equation of the line  is in the

(A) Normal form                      
(B) Point-slope form
(C) Two intercept form
(D) Symmetric form

• Slope of the line 2x + y - 3 = 0 is

(A) 2                   
(B) -2
(C)                
(D) -   

• In the xy-plane, the graph of the inequality 2x > -3 is the

(A) Left half plane      
(B) Right Half plane
(C) Upper half plane
(D) Lower half plane

• The corner point of the boundary lines of inequalities x - y  3 , x + 2y  6 is

(A) (4 1')           
(B) (1 2)
(C) (1 -1)         
(D) (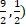

• If (1,2) and (2,3) are ends of a diameter the equation of the circle is

(A) (x - 1)(y - 2) + (x - 2)(Y - 3) = 0
(B) (x - 1)(x - 2) + (y - 2)(y - 3) = 0
(C) (x + 1)(x + 2) + (y + 2)(y + 3) = 0
(D) None of these

• The directrix of the parabola x² = 5 is

(A) y =-5                
(B) x =(C) y =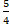       
(D) y =

• The circle is a special case of an ellipse with eccentricity

(A) 0                   
(B)
(C) 1                   
(D)

• Which of the following are the direction angles of a vector?

(A) 45°, 45°, 60°
(B) 30°, 45°, 60°
(C) 45°, 60°, 60°
(D) 30°, 30°, 45°

• The value of scalar triple product 2 x 2.  is

(A) 4    
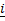
(B) 4
(C) 4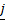                                       
(D) -4

• The work done by the force 2 x 4 in moving a body from A (0,0) to B (3,5) is

(A) 6                   
(B) 32
(C) 13                  
(D) 26

• The range of the function y = coshx is

(A) (-∞,+∞)          
(B) (1,+∞)
(C) (1, +∞)            
(D) 10, +∞)

• The  function f(x) = 4x - x²   is increasing in the interval

(A) 0 ≤ x ≤ 2           
(B) 2 ≤ x < 4
(C) 0 < x < 2           
(D) 0 < x ≤ 2

• dx=

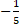
(A)  + c
(B)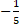  + c
(C)  + c
(D)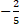  + c

• The equation of the vertical line through  (-5, 3) is

(A) x = -5             
(B) x = 5
(C) y = 3        
(D) y = -3

MATHEMATICS HSSC-II
Section-B
(Mark 40)

Q.2 Attempt any TEN parts. All parts carry equal marks

• Prove the identity sech²x = 1 - tanh²x.
  
• If g(x) = (x² + 1)² find gog(x)?
  
• If y = tan(pTan^-1 x), show that (1 + x²)yi - p(1 + y²) = 0
  
• Find the lengths of the side of a variable rectangle having area 36cm2 when its perpendicular is minimum.
  
• If f(x) =. then find |
  
• Evaluate
  
• Using the method of substitution, evaluate
  
• Find the distance between the parallel lines x + 2y - 5 = 0, 2x + 4y = 1
  
• Find an equation of the line through the point (2, -9) and the intersection of lines 2x + 5y - 8 ≠ 0   and 3x - 4y - 6 = 0
  
• Find the length of the tangent drawn from the point (-5, 4) to the circle. 5x² + 5y² - 10x + 15y - 131 = 0
  
• Write an equation of the parabola with elements: focus (-3, 1); directrix x - 2y -3 = 0
  
• Find the equation of the hyperbola with centre (2, 2) horizontal transverse axis of length 6 and eccentricity  e = 2.
  
• Solve the differentiatial equation  + 2st = 0.
  
• Find angle between the vectors = 2 -  + and =+

SECTION — C
(Marks 40)

Attempt any Five questions. All questions carry equal marks.

Q.3. Prove that =logea

Q.4. Prove that y + x = 0 if x =  , y =

Q.5. Evaluate 

Q.6. If two verticles of an equilateral triangle are A(-3,0) and B (3,0), find the third vertex. How many of these triangles are possible.

Q.7. Graph the feasible region of the system of linear Inequalities and find the corner points ;

            3x + 2y ≥6, x+y≤ 4, x ≥ 0, y ≥ 0

Q.8. Find the equation of the tangent to the circle x² +y² = 25 through (7, -1)

Q.9. Prove that the points whose position vectors are

A(-6 + 3  + 2), 
B(3 -2  + 4),
C(5  -7 + 3),    
D(-13  +17 - )