Gujranwala part1
Board 2014
Mathematics Time: 30 Minutes
Paper I
(Objective) Marks: 20
Note: You have four choices for each objective type question as A; B, C and D. The choice which you think is correct, fill that circle in front of that question number with marker or pen on the answer book provided. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank.

Q.1

• The number of terms in the expansion of (a + b)ⁿ is

(A) n
(B) n + 1
(C) n – 1
(D) n + 2

• The sum of an infinite geometric series exists if

(A) |r|<I
(B) |r|>I
(C) |r|=I
(B) Ir|= 0

• If cosx =  , then reference angle is

(A)
(B)
(C)
(D)

• The number of roots of a quadratic equation is

(A) 1
(B) 2
(C) 3
(D) 4

• The value of sin (cos^-1 ) is

(A)
(B)
(C)
(D)

• Sin 5θ + sin 3θ is equal to

(A) 2 cos 2θ sinθ 
(B) -2 cos 4θ sinθ 
(C) -2 sin 4θ cosθ 
(D) 2 sin 4θ cosθ 

• If p and q are two statements, then p∩q represents

(A) disjunction
(B) conjunction
(C) conditional
(D) biconditional

• Multiplicative identity of complex number is

(A) (0, 0)
(B) (0, 1)
(C) (1,0)
(D) (1,1)

• If A and B are independent events and P(A) = and  P(B) =  then P(A∩ B) is

(A)
(B)
(C)
(D)

• Partial fractions of  , are of the form

(A)
(B)
(C)
(D)

• In one hour, the hour hand of a clock turns through

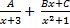
(A)
(B) radians
(C)  radians
(D)  radians

• If A = , then |A| is equal to

(A) 5
(B) 20
(C) 14
(D) 6

• Union of set of rational and irrational numbers is set of .

(A) whole numbers
(B) complex numbers
(C) real numbers
(D) natural numbers

• If  ABC is right angle triangle, the law of cosines reduces to

(A) the law of sines
(B) area of triangle
(C) the law of tangents
(D) the pythagoras theorem

• ⁿC_r is equal to
  

(A) (B)
(C) n
(D)

• In the expansion of ()²  middle term is x

(A) T₆
(B) T₇
(C) T₈
(D) T₅

• If a polynomial P(x) = x³ +4x² -2x +5 is divided by x - 1, then the remainder is

(A) 4
(B) -2
(C) 5
(D) 8

• Range of cos x is

(A) [-1,1]
(B) [0, ∞]
(C) [-∞,0]
(D) [-∞, ∞]

• If A is a matrix of order 3 x 2, then order of At is

(A) 2 x 3
(B) 3 x 3
(C) 2 x 2
(D) 3 x 2

Inter (Part-I)
Gujranwala Board 2014
Mathematics
Paper I
(Subjective)
Time: 2:30 hours
Marks: 80
Note: Section 1 is compulsory Attempt any three (3) questions
Section II.

Q.2
Write short answers to any EIGHT questions: (2 x8=16)

• Define an irrational number.
• Simplify:    (i)¹⁰¹
• Write the power set of A = (0, 1}
• Write the truth table of p  (p V q).
• Define an onto function.
• Give an example of a group w.r.t addition + ).
• Define the order of a matrix.
• Find A ^-1 if A =
• Find x if
• Solve: x (x +7) = (2x - 1)(x + 4)
• State Remainder Theorem
• Evaluate (1 +  - ) (1 –  + )

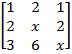
3.Write short answers to any EIGHT questions: (2x8=16)

• Define proper fraction.
• Find next two terms of sequence 1,-3, 5,-7………
• Which term of A.P, 5,2,-1,..... ..is -85 ?
• Find sum of infinite G.P. 2, 1…….
• Find H  if a =2, b  = 6
• Find the value of n when 11Pn = 11 . 10.9
• Prove that _nC^r = ⁿC_n-r
• Define probability.
• Write formula of P(A∩B) where A and B are independent events.
• Show that  represents an integer for n = 2, 3
• Evaluate (9.98)1/2 by binomial theorem to three places of decimal.
• Find the middle term in the expansion of 12

4.Write short answers to any NINE questions: (2 x 9 =18)

• Find  when θ= radian, r = 6 cmI .
• Prove that:     = 2 sec2 θ
• Show that: 
• Without using table calculator, find the value cos 75o.
• Prove that :  = tan A
• Express sin 5 x + sin 7 x as a product.
• A ladder leaning against a vertical wall makes an angle of 24° with the wall. If its foot is 5 to from the wall, find its length.
• Find the period of sin
• Find the area of triangle ABC in which b =  21.6 ,c= 30.2 , α= 52° 40'
• Define in-circle.
• Find the value of the expression (sin-1
• Complete the formula            sin^-1 A+ sin^-1  B = 
• Find the solution of the equation cosec θ = 2 which lies in [0, 2 .

(SECTION-II)

Q.5
(a) If 'A' is symmetric or skew symmetric, then show that A2 is symmetric. (5)
(b) Solve the equation:            2x +20-x+6 -20 =0 (5)
Q.6
(a) Resolve   into partial fractions. (5)
(b)Sum the series        1 + 4- 7 + 10 + 13 - 16 + 19 + 22 - 25+........to 3 n terms. (5)
Q.7
(a) Determine the probability of getting two heads in two successive tosses of a balanced coin. (5)
(b) Find the term independent of x in the expansion of  x in the expansion of (x - )10  (5)
Q.8
(a) Prove the identity: sin6θ- cos6θ  = (sin² θ cos² θ)(1-sin² θ-cos² θ). (5)
(b) Reduce sin4θ to an expression, involving only function of multiple of θ) raised to the first power.(5)
Q.9
(a) Prove that: = 4   R cos   cos  cos  (5)
(b) Prove that : tan^-1 tan^-1 + tan^-1  = tan^-I  + tan^-1    (5)