Inter(Part 11)
Gujranwala
201 4
Mathematics
Paper II (Objective)
Time: 30 Minutes
Marks: 20
Note: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct, fill that circle in front of that question number with marker or pen on the answer book provided. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank.
Q.1
(A) j
(B) i
(C) -i
(D) -j
(A) scalar quantity
(B) unit vector
(C) vector quantity
(D) null vector
(A) 0 < e < 1
(B) e = 1
(C) e > 1
(D) e = -1
(A) c2 + a2 (1 + m2)
(B) c2 = a2 (1 - m2)
(C) c2= a2 (m2 -1)
(D) c + a2 (1 + m2)
(A) (1,4)
(B) (1,3)
(C) (1,4)
(D) (3,1)
(A) x = k
(B) y = k
(C) x + y = k
(D) x-y=k
(A) one
(B) finite
(C) infinite
(D) three
(A)
| +c
(B)|x| +c
(C)+c
(D) -1x-2 +c
(A)
(B)+c
(C)+c
(D)+c
(A) sec x tanx +c
(B)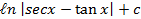
(C)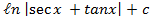
(D) secx + tanx +c
(A) [f(x)]n+1+c
(B)+c
(C) [f(x)]n+1+c .(n+1)+c
(D) n[f(x)]n+1+c
(A)
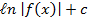
(B)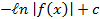
(C)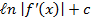
(D)
(A) -5
(B) 5
(C) 0
(D) 1
(A)
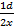
(B) 2x
(C)
(D)
(A)
(B) f’ (x)< 0
(C) f’ (x) > 0
(D) f’ (x) =0
(A) 0
(B) 1
(C) -1
(D) does not exist
(A) f(x)
(B) f’(x)
(C)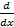
(D) D(f(x))
(A) 5 (2x2 +3)4
(B) 5(2x2 + 3)4 .4
(C) 5 (2x2 +3)4 .3
(D) (2x2+3)4 .20x
(A) even function
(B) odd function
(C) neither even nor odd
(D) cubic function
(A) -1
(B) 1
(C) 2
(D) 0
Inter(Part-lI)
Gujranwala Board 2014
Mathematics Time: 2:30 hours
Paper r II
(Subjective) Marks: 80
(SECTION-2)
Q.2
Write short answers to any EIGHT questions: (2x8=16)
Q.3
Write short answers to any EIGHT questions:(2x8=16)
Q.4
Write short answers to any NINE question : (2x9=18)
(SECTION –II)
Q.5
(a) Find the values m and n, so that function f(x) is continuous at x=3 where . (5)
F (x) = 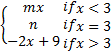
(b) If y = a cos (![]() +b sin (
+b sin (![]() prove that:(5)
prove that:(5)
X2![]() + x
+ x ![]() +y=0
+y=0
Q.6
(a) Evaluate I = ![]() sin x dx (5)
sin x dx (5)
(b) Find an equation of the line through the intersection of the lines x+2y +3=0, 3x +4y +7 = 0 and making equal intercepts on axes. (5)
Q.7
(a) Evaluate ![]() dθ (5)
dθ (5)
(b) Maximize f(x,y) = x+3y subjected to constraints
2x +5y ![]() 30; 5x +4y
30; 5x +4y ![]() 20; x
20; x ![]() 0;y
0;y ![]() (5)
(5)
Q.8
(a) Find the equation of a circle passing through the points A4,5) B(-4,-3), C(8,-3) (5)
(b) Find two vectors of length 2 parallel to the vector v =2i -4j +4k. (5)
Q.9
(a) Find the centre, foci, eccentricity and vertices of hyperbola ![]() =I (5)
=I (5)
(b) Use vector method to prove that sin (a-![]() ) = sin a cos
) = sin a cos ![]() cos a sin
cos a sin![]() . (5)
. (5)