Mathematics
Paper II
(Objective Type)
2014
Time Allowed: 30 Minutes
Max. Marks: 20
(Group-I)
Note: Four possible answers A, B, C and D to each question are given. The choice which you think is correct, fill that circle in front of that question with Marker or Pen ink. Cutting orfilling two or more circles will result in zero mark in that question.
(A)
+c
(B)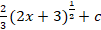
(C)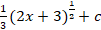
(D)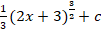
(A) (-3, 2)
(B) (3 - 2)
(C) (3, 2)
(D) (-3, -2)
(A) 0
(B) 2
(C) 4
(D) 6
(A) 0
(B)
(C)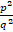
(D)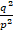
(A) 2x+h
(B)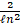
(C) 2x.n2
(D)2x
(A)
n cosx + c
(B)n sin x + c
(C) -n cosx + c
(D) -nsinx + c
(A) 0
(B) 1
(C) x + 2
(D) x - 2
(A)2x+y>5
(B)2x+y5
(C)2x+y<3
(D)2x+y<5
(A)
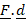
(B)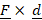
(C)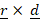
(D)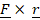
(A)
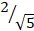
(B)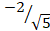
(C)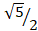
(D)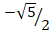
(A)
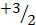
(B)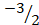
(C)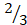
(D)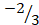
(A) esinx.cosx
(B) esinx .sin x
(C) sin x esinx-1
(D) sin xesinx+1
dx equals:
(A) e-x.
x
(B) e-x .+
(C) ex.+c
(D) e-x.nx+c
is equal to:
(A) sin x
(B) cos x
(C) sinh x
(D) cosh x
dx equals:
(A)
n (
nx) + c
(B)nx + c
(C)n
+ c
(D)n
+ c
Solution of y.dx + x.dy = 0 is equal to :
(A) x . y = Constant
(B)= Constant
(C) x + y = constant
(D) x - y = constant
If y =
,then
equals:
(A) tan x
(B) cot x
(C) - tan x
(D) - cot x
X-co-ordinate of centroid of triangle ABC with A (-2 , 3) B (- 4, 1 ) : C (3, 5 ) equals :
(A) -1
(B) 1
(C) 3
(D) -3
(tan x) is equal to:dx
(A)
cos x
(B)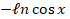
(C)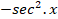
(D)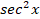
dx equals:
(A)
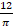
(B)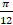
(C)
(D)
Inter Part-II
Lahore Board 2014.
Mathematics
Paper H (Essay Type)
Time Allowed: 2.30 hours
Max. Marks: 80
(Group-I)
(SECTION-I)
2.Write short answers to any EIGHT (8) questions : 16
3. Write short answers to any EIGHT (8) questions : I6
4. Write short answers to any NINE (9) Questions : 18
(SECTION-II)
Attempt any THREE questions.
5.(a) If ![]() find the value of k. so that f is continuous at x = 2
find the value of k. so that f is continuous at x = 2
(b) Differentiate ![]() w.r.t
w.r.t ![]()
6.(a) Evaluate ![]()
(b) Find an equation of the perpendicular bisector of the segment joining the points A (3, 5) and B (9, 8) 5
7.(a) Solve differential equation 1 + cos x tan y ![]() = 0
= 0
(b) Minimize z = 2x+ y subject to the constraints x+y≥3 , 7x+ 5y≤35 ,x≥0 ,y≥0
8.(a) Write equations of tangent- lines to the circle x2 + y2 + 4x+ 2y = 0 drawn from the point P (-1, 2). Also find the tangential distance.
(b) Prove by using vectors that the line segment joining the mid points of two sides of a triangle is parallel to the third side and half as long.
9.(a) Show that the equation x2 + 16x + 4y2 - I6y + 76 = 0 represents an ellipse. Find its foci eccentricity, vertices and directrices.
(b) A focus magnitude 6 units acting parallel to 2![]() displaces the point of application from (1, 2, 3) to (5,3,7 ) find the work done.
displaces the point of application from (1, 2, 3) to (5,3,7 ) find the work done.