INTERMEDIATE (12TH CLASS-2014)
PART-I
MATHEMATICS
GROUP-I
TIME ALLOWED:30
MAXIMUM MARKS:20
OBJECTIVE
Note: You have four choices for each objective type question us A, B, C and D. The choice which you think is correct, fill that circle in front of that question number. Use marker or pen to fill the circles, Cutting or filling two or more circles will mull in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case .BUBBLES are not filled. Do not solve question on this sheet of OBJECTIVE PAPER.
Q.No.1
A. ln(tan-1 x)+c
B. Ln(tanx)+c
C. Tan-1x+ c
D. Tanx +c
A.
B.
C.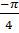
D.
A.
B.
C.
D.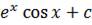
A. M1.m2 = -1
B. M1-m2 = 1
C. M1+m2 = 0
D. M1-m2 = 0
A. (1,2)
B. (-1,2)
C. (-1,-2)
D. (1,1)
A. (1,1)
B. (-2,1)
C. (1,2)
D. (-2,3)
A. (0,a)
B. (0,-a)
C. (a,0)
D. (-a,0)
A.
x
B.x
C..
D..
A. 0
B. 1
C. -1
D. 2
A. Odd function
B. Even function
C. Explicit function
D. Implicit function
A. 0
B. -1
C. 1
D. 3
A. x
B.
C. a\ln a
D. ax/lna
A.
B.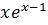
C.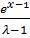
D.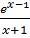
A. Cosx3
B. -Cosx3
C. X2Sin x3
D. 3 X2 Cosx3
A.
B.
C.
D.
A. Sinx + Cosx
B. (Sinx + Cosx)2
C. Sinx-Cosx
D. (Sinx-Cosx)
A. -Cosec2x + c
B. Cosec2 x+c
C. ln Cosx+c
D. ln Sinx+c
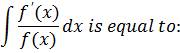
A.
B.
C.
D.
A.
+c
B.+c
C.+c
D.+c
INTERMEDIATE (12TH CLASS-2014)
PART-I
MATHEMATICS
GROUP-I
TIME ALLOWED:2:30
MAXIMUM MARKS:80
Subjective
NOTE:write same question number and its part number on answer book,as given in the question paper.
SECTION-I
2. Attempts any eight parts.8x2=16
3. Attempts any eight parts. 8x2=16
4. Attempts any nine parts.
SECTION-II
Note: Attempts any three questions. 3x10=30
5.(a) Discuss the countinuity of f(x) =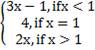 at c = 1
at c = 1
(b) if x= Sinθ, y= Sinmθ,Show that (1-x2)y2-xy1+m2y=0
6.(a) Evaluate ![]() dx
dx
(b) Find the points trisecting the joints of A(-1,4) and B(6,2).
7.(a) Evaluate ![]() dx
dx
(b) Graph the feasible region and fid the corner points of the following system of in equalities(subject to the constraint)
x-y ≤3, x+2y≤6, x≥0,y≥0
8(a) Show that the circles x2+y2+2x-8=0 and x2+y2-6x+6y-46=0
(b) by using vector ,prove that the mid point of hypotenuse of a right triangle is equidistant from its vertices.
9.(a) Find the center ,foci ,eccentricity vertices and equation of directories of ![]() -
-![]() = 1
= 1
(b) Prove that four points A(-3,5,-4) ,B(-1,1,1), C(-1,2,2) and D(-3,4,-5) are coplanar.
Paper Code
Number:4195
2014(A) ROLL.NO: ____________
INTERMEDIATE PART-II (12TH CLASS)
MATHEMATICS PAPER –IIGROUP-II TIME ALLOWED:30 minutes
MAXIMUM MARKS:20
OBJECTIVE
Note: You have four choices for each objective type question us A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles, Cutting or filling two or more circles will mull in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case BUBBLES are not filled. Do not solve question on this sheet of OBJECTIVE PAPER.
Q.No.1
A.
+C
B.+C
C.+C
D.+C
A.
B. ln+c
C. lnf’(x)+c
D. f’(x)lnf(x)+c
A.
B. 4
C. 2
D. 1
A.
B.
C.
D. -
A. Y= x
B. Y= c
C. Y=
D. Y= c
A. 0
B. 1
C.
D.
A.-2
B. 2
C. 3
D. 1
A. 2x+1>0
B. 2x+1<0
C. 2x+10
D. 2x-1 > 0
A. X2-y2 =7
B. X2+ y2 =7
C. X2+ y2=0
D. X2+ y2 =1
A. (h,k)
B. (-h,-k)
C. (-h, k)
D. (h, -k)
A. 8
B. 2
C. 1
D. 4
A. 4i+5j
B. -4i+5j
C. 4i-5j
5i-4j
A. -f(x)
B. F(-x)
C. F(x)
D. None of these
A. F’(x)
B. F’(a)
C. F’(2)
D. F’(0)
A. 0
B. 1
C. E
D.
A. 100
B. 90
C. 50
D. 0
A.
x
B.x
C.x
D.x
A. -
B. Sin2x
C. Cos2x
D. Sec2x
A. F”( C ) > 0
B. F”( C ) < 0
C. F”( C ) = 0
D. F”( C ) ≥ 0
A. Cosx+c
B. -Cosx+c
C. Sinx+c
D. -Sinx+c
INTERMEDIATE PART-I
(11TH CLASS-2014)
MATHEMATICS
GROUP-II
TIME ALLOWED:2:30
MAXIMUM MARKS:80
Subjective
NOTE:write same question number and its part number on answer book,as given in the question paper.
SECTION-I
2. Attempts any eight parts. 8x2=16
3. Attempts any eight parts. 8x2=16
4. Attempts any nine parts.
SECTION-II
Note: Attempts any three questions. 3x10=30
5.(a) Show that the parametric equations x=a Cos θ, y=b Sin θ represent the equation of ellipse ![]() =1
=1
(b) Differentiate ![]() w.r.t
w.r.t ![]() .
.
6.(a) Evaluate ![]() xdx
xdx
(b) Determine the value of P ,such that the lines 2x-3y-1=0,3x-y-5=0 nad 3x+py+8=0 meet at a point.
7.(a) Solve (sin y +cos y)dy =[x(2lnx+1)]dx
(b) Maximize the function defined as f(x,y) =2x+3y subject to the constraints 2x+y≤8, x+2y≤14 x≥0,y≤0
8.(a) Find an equation of the circle passing through the points A(4,5),B(-4,-3),C(8,-3)
(b) Prove by vector method that Cos (![]() )=Cos
)=Cos![]() Cos
Cos![]() -Sin
-Sin![]() Sin
Sin![]() .
.
9(a) Find the equation of an ellipse with Foci (±3,0) and minor axis of length 10.
(b) a A force of magnitude ‘6’ units acting parallel to 2![]() -2
-2![]() +
+![]() displaces, the point of application from (1,2,3) to(5,3,7).Find the work done.
displaces, the point of application from (1,2,3) to(5,3,7).Find the work done.