RAWALPINDI
BOARD 2014
PAPER MATHEMATICS
PART-ITime: 30 Min.
(Objective Part1)
Marks: 20
Note: Four Answers are given against each column A,B,C & D. Select the write answer and only separet answer sheet, fill the circle A,B,Cor D with pen or marker in front of that question number.
- For quadratic equation ax2+bx+c=0, the sum of its roots is:
(a) 
(b) 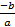
(c) 
(d) 
- Partial fraction of
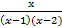 will be:
will be:
(a) 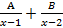
(b) 
(c) 
(d) 1+ 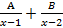
- Common difference of A.P. 17, 13, 9, …………. is:
(a) 4
(b) -4
(c) 30
(d) 15
- Arithmetic Mean between
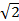 and 3
and 3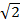 is:
is:
(a) 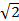
(b) 2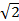
(c) 6
(d) 3
- The multiplicative inverse of non-zero real No. is:
(a) 0
(b) a
(c) -a
(d) 
- If A = {}, the P(A) is equal to:
(a) Infinite set
(b) Singletion set
(c) Empty set
(d) Null set
- The additive inverse of a matrix A is:
(a) A
(b) -A
(c) A2
(d) 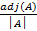
(a) -2
(b) 2
(c) 0
(d) 3
- If x2+ 3x+ 7 is divided by x + 1, remainder is:
(a) -5
(b) 11
(c) 5
(d) -11
(a) s∆
(b) 
(c) 
(d) 
- sec(cos-1
 ) is equal to:
) is equal to:
(a) 
(b) 2
(c) 
(d) 
(a) sec2θ
(b) 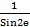
(c) tan2θ
(d) 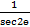
(a) 36
(b) 360
(c) 6
(d) 4
(a) 18
(b) 12
(c) 6
(d) 0
- The inequality n!> 2"-1 is valid if:
(a) n = 3
(b) n ≤ 3
(c) n< 4
(d) n ≥ 4
- Which angle is quadrantal angle?
(a) 120o
(b) 270o
(c) 60o
(d) 45o
- If sinɵ=
 , then ɵ is:
, then ɵ is:
(a) 30°
(b) 45°
(c) 90°
(d) 120°
(a) -cos 33°
(b) sin 41°
(c) -sin 41°
(d) sin 16°
(a) 
(b) 
(c) 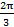
(d) π
Time: 2:30 Hours
(Subjective Part)
Marks: 80
SECTION-I
2. Attempt any Eight Parts.
- Show that Ѵz € c, z.z=│z│2
- Define the terms proper subset and improper sub set.
- What is the diagonal matrix?
- Solve by using quadratic formula 15x2 + 2ax – a2 = 0
- Verify without expansion│α β + γ 1│ = 0
│β γ + α 1│
│γ α + β 1│
- Evalualte(1+w+w2)8:-
- Does the set (1,-1} possess closure property w.r.t. addition and multiplication?
- Find thy inverse and tell whether inverse is a function or not, if
A={(2,1),(7,8),(8,7),(4,3)}.
- A number exceeds it square root by 56, find the number.
- Define the terms upper triangular and lower triangular matrix.
- Check whether the given martrix is singular or not, if:-
A= 
- If α, β are roots of equaiton 3x2- 2x + 4 = 0, find
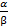 +
+ 
3. Attempt any Eight Parts.16
- Define the rational fraction.
- Resolve
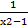 into partial fraction.
into partial fraction.
- Define Hamonic Mean between "a" and "b".
- Insert four real geometric mean between 3 and 96.
- Find "n", if nP2 = 30.
- Evaluate 3
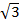 correct to three places of decimals.
correct to three places of decimals.
- If the 5th term of an A.P. is 13 and 17th term is 49, find a13.
- If 5,8 are two A.M. between "a" and "b", find "a" and "b".
- In how many ways can a necklace of "8" beads of different colours be made?
- How many diagonals can be formed by joining the vertices of a polygon having 8
sets?
- Find the probability if there are 5 green and 3 red bails in a box, one ball is taken out
and ball is green.
- Determine the middle term in the expression of
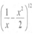
4.Attempt any sine Parts.18
- Prove that
 = (cosecɵ + cotɵ)2
= (cosecɵ + cotɵ)2
- Prove that
 = tan37o
= tan37o
- Find the period of cos

- Find the value of sin2α, if cosα=
 , where 0 < α <
, where 0 < α < 
- Prove that R=
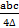 .
.
- Solve the equation sinx=

- Solve for solution set, if the equation is sinx + cos 3x = cos5x.
- If tanɵ =
 and the terminal arm of the angle is not in the III quadrant, find the value
and the terminal arm of the angle is not in the III quadrant, find the value
of 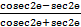
- Express product as sum or differences of sin(x+45o)sin (x-45o).
- At the top of a cliff 80m high, the angle of depression of a boat is 12o. How far is the
boat from the cliff?
- Solve the triangle ABC in which: b = 95;c = 34;α = 52o.
- Find the measure of the greatest angle, if sides of the triangle are 16,20,30.
- Without using the table and calculator, find the value of tan (-135o)
SECTION-II:
Attempt any THREE questions. Each question carries 10 marks.
Q.5
(a) Prove that set of a 4 fourth roots of unity {1,-1,i,-i} is a group with respect to
multiplication.
(b) Solve the matrix equation 3x-2A= B, if:
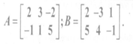
Q.6
(a) lf the roots of px2+ qx +q= 0 are α and β, then prove that:
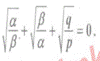
(b) Resolve into partial fraction 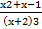
Q.7
(a) If H.M. and A.M. between two numbers are 4 and that  respectively.Find the
respectively.Find the
numbers.
(b) Use binomial theorem to show that:
1+  +
+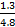 +
+  + ……….. =
+ ……….. = 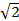
Q.8
(a) Prove the identity 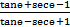 =tanɵ+secɵ
=tanɵ+secɵ
(b) Prove that 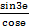 +
+ 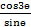 = 2cot2ɵ.
= 2cot2ɵ.
Q.9
(a) Solve the trianle ABC if α = 53, β = 88o36, γ= 31°54'.
(b) Prove that: 2tan-1  + tan-1+
+ tan-1+  =+
=+ 
![]()
![]()
![]()
![]()

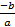

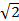
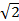
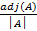
![]()
![]() bcsina
bcsina![]()
![]() ac
ac 





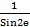
![]()
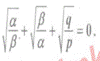
![]()
![]() respectively.Find the
respectively.Find the ![]() +
+![]() +
+ ![]() + ……….. =
+ ……….. = ![]()
![]() =tanɵ+secɵ
=tanɵ+secɵ![]() +
+ ![]() = 2cot2ɵ.
= 2cot2ɵ.![]() + tan-1+
+ tan-1+ ![]() =+
=+ ![]()