RAWALPINDI
BOARD 2014
PAPER MATHEMATICS
PART-II
Time: 30Min
(Objective Part)
Marks: 20
Note: Four Answer are given against esch column A,B,C & D. Select the write answer and only separet answer sheet, fill the circle A,B,C or D with pen or marker in front of that question number.
(a) 
(b) 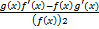
(c) 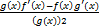
(d) 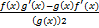
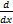 (
(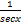 ) is equal to:
) is equal to:
(a) 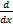 Sinx
Sinx
(b) 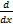 cosecx
cosecx
(c) 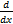 cosx
cosx
(d) 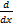 cotx
cotx
 (cosec-1x) is equal to:
(cosec-1x) is equal to:
(a) 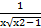
(b) 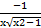
(c) 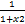
(d) 
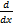 (Inx) is equal to:
(Inx) is equal to:
(a) 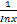
(b) 
(c) x
(d) Inx
- ʃsec5xtan5xdx is equal to:
(a) 5sec5x + c
(b) 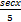 +c
+c
(c) 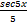 +c
+c
(d) 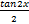 +c
+c
(a) -2sin 2x+c
(b) 2sin 2x +c
(c) 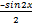 +c
+c
(d) 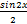 +c
+c
- If f(x) = cosx, then f(0) =?
(a) -1
(b) 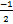
(c) 0
(d) 1
(a) ex + e-x
(b) ex - e-x
(c) 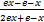
(d) ) 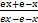
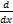 (x3) is equal to:
(x3) is equal to:
(a) ) 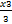
(b) x2
(c) 3x2
(d) 4x4
- The lines l1,l2 with slopes m1,m2, are perpendicular if:
(a) m1,m2=-1
(b) m1 = m2
(c) m1 + m2= 0
(d) m1m2 = 1
- Which one is not a solution of in-equality 2x + 3y < 0?
(a) (-1,-2)
(b) (1, +2)
(c) (2,3)
(d) (0,1)
- The centre of the circle x2 + y2 + 2gx + 2fy + c = 0 is:
(a) (g,f)
(b) (f,g)
(c) (-f,-g)
(d) (-g,-f)
- The set of all the points in a plane which are equidistant from a fixed point and
fixed the is called:
(a) circle
(b) ellipse
(c) parabola
(d) hyperboia
(a) i
(b) 1
(c) -1
(d) j
(a) 1
(b) 0
(c) -1
(d) 2
(a) 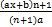 + c
+ c
(b)  + c
+ c
(c)  + c
+ c
(d) 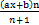
- If 1ʃ0(4x + k) dx=4, then k will be:
(a) 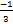
(b) 0
(c) 1
(d) 2
(a) 20
(b) 80
(c) 28
(d) 2
- Degree of differential equation
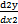 +
+ 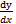 - 3x = 0 is:
- 3x = 0 is:
(a) 1
(b) 2
(c) 0
(d) 3
- The slope of a line wish inclination 90o is:
(a) 0
(b) 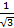
(c) 1
(d) Undefined
Time: 2:30 Hours
(Subjective Part)
Marks: 80
SECTION-I
2. Attempt any Eight Parts.
- Evaluate lim
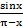 .
.
x→π
- Evaluate lim
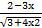 .
.
x→∞
- Differentiate (
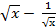 )2 w.r.t.’x’
)2 w.r.t.’x’
- If y=
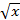 +
+  , then find
, then find 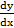
- Differentiate sin3x w.r.t cos2x
- If y =
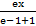 , then find
, then find 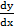
- If y = Sin-1 (
 ), then find y2.
), then find y2.
- Define power series.
- If x = at2, y = 2at, find
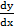 .
.
- If y = In (x+
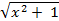 ), find
), find 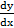
- Find by definition, the derivative w.r.t ‘x’ of x40
- Determine the interval in which f is increasing or decreasing
f (x) = x3 + 3x + 2, x €(-4,1)
3. Attempt any Fight Parts.
- Evaluate ʃsin2xdx
- Evaluate ʃ
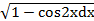
- Evaluate ʃ
 dx
dx
- Evaluate ʃe3x(
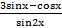 ) dx
) dx
- Evaluate ʃInxdx
- Evaluate 3ʃ0
 dx
dx
- Evaluate 6ʃ0cos3ɵdɵ
- Define the optimal solution
- Solve the differential equation (ex + e-x)
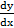 = ex – e-x
= ex – e-x
- Find the area above the x-axis, bounded by the curse y2 = 3-x from x=-1 to x=2
- Graph the solution set of the linear inequality 2x + 1 ≥ 0.
- Find δy and dy of the function y = x2 +2x when x changes from 2 to 1.8.
4. Attempt any Nine Parts.18
- The xy coordinate axes are rotated about origin through an angle of 30". If xy
coordinates of a point are (5,7), find its xy coordinates.
- The length of perpendicular from origin to a line is 5 units and inclination of this
perpendicular is 120o. Find equation of this line.
- Check whether the origin and the point (5, -8) lie on the same side or opposite side of
the line 3x + 7y + 15 = 0.
- Transform the equation 5x – 12y + 39 = 0 into slope-intercept form.
- Find the angle front the line line with slope
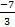 to the line with slope
to the line with slope  .
.
- Write an equation of the circle with centre (-3,5) and radius 7.
- Write down the equation of tangent and normal to the circle x2+y2=25 at point(4,3)
- write an equation of parabola having focus (-3,1) and direct x-2y-3=0.
- Find foci, directix of ellipse 25x2+9y2= 225.
- Find 'α' if │αi + (α+1)j + 2k│=3
- Prove that: μ.(v x w) + v.(w x μ) + w.(μ x v) =3μ.(v x w)
- Find the projection of a along b when A – I – p = j
- Find volume of tetrahedron with the vertices
A(0,1,2), B(3,2,1), C(1,2,1) and D(5,5,6).
SECTION-II
Attempt any THREE questions, Each questions carries (10 marks)
5.(a) Prove that lim 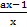 = loge a
= loge a
x→0
(b) If y= ex sin x, show that 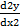 - 2y
- 2y 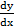 +2y = 0
+2y = 0
6.(a) Evaluate ʃ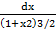
(b) Find h such that A(-1, h), B(3,2) and C(7,3) are collinear.
7.(a) Evaluate 3ʃ-1│x-3│dx
(b)Maximize f (xy) = x +3y subject to the constraints
2x+ 5y≤30,5x+ 4y≤ 20,x≥0, y≥ 0.
8.(a) Find the coordinates of the points of intersection of the line
x+ 2y = 6 with the circle x2+y2-2x-2y-39=0
(b)Find a vector of length 5 in the direction opposite to that of V=i-2j+3k:
9.(a) Find an equation of parabola with focus (2,5) and directrix y=1.
(b) Prove by vector method that cos (α + β) = cosα cosβ – sinα sinβ

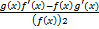
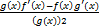
Sinx
cosecx
cosx
cotx
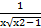
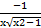
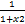
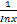

+c
+c
+c
+c
+c
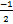
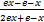
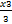
+ c
+ c
+ c
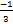
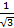
![]() = loge a
= loge a![]() - 2y
- 2y ![]() +2y = 0
+2y = 0 ![]()