SAHIWAL BOARD 2014
PAPER MATHEMATICS
PART-2
Time: 30
(Objective Part)
Mark20
Note:Four Answers are given against each column A, B, C & D. Select the write answer and onto separet answer sheet, fill the circle A, B, C or D with pen or marker in from of that question number.
(a) cosh 3x
(b) -cosh 3x
(C) 3cosh 3x
(d) Coshx
(a) x2x-1
(b) 2x In 2
(c) In 2x
(d) X In 2
(a) (1, + ∞)
(b) (-1, - ∞)
(c) (-1, + ∞)
(d) (-∞, + ∞)
(a) sec2 x
(b) cosec2 x
(c) - cosec2x
(d) –sec2 x
(a) zero
(b) -1
(c) I
(d) 2
(a) Insecx+c
(b) Incosecx+c
(c) In sin x + c
(d) In cot x + c
(a) xsin x-cosx + c
(b) –xcosx + sinx + c
(c) Sin x - COS X + c
(d) sin x+cosx + c
(a)
(b)
(c) 3x
(d)
(a) tan x+c
(b) In cot x + c
(c) cot x+ c
(c) –In cot x + c
(a)
loga e
(b)loga e
(c)loge e
(d)Ina
(a) ax1 + by1 + c < 0
(b) ax1 + by1 + c = 0
(c) ax1+by1+c>0
(d) ax1-by1-c<0
(a) zero
(b)
(c) 1
(d)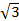
(a) 5
(b) 4
(c) 2
(d) 1
(a) Inx + c
(b) In In In x + c
(c) x+c
(d) 40(In x) + c
(a) ex cos x + c
(b) ex sin x+c
(c) ex tan x + c
(d) ex cot x + c
(a)
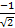
(b)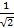
(c)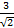
(d)
(a) i
(b) j
(c) 1
(d) k
(a)
=
+
(b)=
-
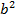
(c)=
+
(d)=
-
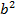
(a) 2x + y
6
(b) x-y > 1
(c) 3x + 5y < 7
(d) 2x+y6
(a) (3,0)
(b) (2,1)
(c) (3, 1)
(d) (0,1)
Time: 2:30 Hours
(Subjective Part)
Marks: 80
SECTION-I
2.Attempt any Eight Parts.16
3.Attempt any Eight Parts.16
4. Attempt any Nine Parts.18
Section-II
Attempt nay three question. Each questions carries 10 marks.
Q.5
(a) Evaluate ![]() .
.
(b)Differentiate y = sin ![]() w.r.t. ‘x’
w.r.t. ‘x’
Q.6
(a) Find ![]()
![]() dx
dx
(b) Find lines represented by 2x2 +3xy – 5y2 = 0
Q.7
(a) Evaluate![]() θdθ .
θdθ .
(b) Find the solution set of inequalities x+ y ![]() 5 and x – y
5 and x – y ![]() 1.
1.
Q.8
(a) Find the equations of tangents drawn from point (-7,-2) to circle (X+1)2 + (y -2)2 = 26.
(b )Find cosine of angle ![]() between
between ![]() and
and ![]() where
where ![]() = 3
= 3![]() +
+ ![]() -
- ![]() ,
, ![]() = 2
= 2![]() -
- ![]() +
+ ![]() .
.
Q.9
(a) The major axis of an ellipse in standard form lies along the x-axis and has length 4![]() .The distance between foci equals the length of the minor axis. Write an equation of the ellipse.
.The distance between foci equals the length of the minor axis. Write an equation of the ellipse.
(b) Find volume of the tetrahedron with the vertices (0,1,2), (3,2,1), (1,2,1) and (5,5,6).