Mathematics
(Objective)
Group-I
(Common for Old & New Scheme)
Paper (I)
Time Allowed:-30 minutes
PAPER CODE 2193
Maximum Marks: 20
Note : You have four choices for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. Write PAPER CODE, which is printed on this question paper, on the both sides of the Answer Sheet and fill bubbles accordingly, otherwise the student will be responsible for the situation. Use of link Remover or white correction fluid is not allowed.
(A) 300
(B) 450
(C) 600
(D) 150
(A) 1
(B) -1
(C) ι
(D) -ι
(A) A∪B
(B) A'∩B'
(C) A'∪B'
(D) A∩B
(A) Semi-group
(B) Commutative group
(C) Symmetric group
(D) Group
(A) 3x2
(B) 2x3
(C) 2x2
(D) 3x3
(A) 2
(B) 4
(C) 6
(D) 8
(A) line
(B) Parabola
(C) Triangle
(D) Rectangle
(A) -
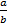
(B)
(C)
(D) -
(A) proper fraction
(B) improper fraction
(C) Equation
(D) Identity
(A) 1,3,6…….
(B) 2,3,5…..
(C) 1,3,5…...
(D) 5,3,1…..
(A) Ist term
(B) Middle term
(C) Tenth term
(D) Last term
(A) {H}
(B) {T,T}
(C) {H,H}
(D) {H,T}
(A) 1
(B)
(C) 2
(D)
(A)
th
(B)th
(C)th
(D) )th
(A) n ≥ 3
(B) n ≥ 2
(C) n ≥1
(D) n < 3
(A)
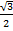
(B)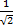
(C)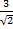
(D) 1
(A) 2Cos2α+1
(B) 2Cos2α-1
(C) 2Sin2α+1
(D) 2Sin2α-1
(A)
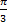
(B)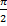
(C)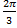
(D) π
(A)
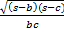
(B)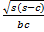
(C)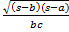
(D)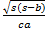
(A) Cot-1x
(B) (Cot x)-1
(C) Tan x
(D) (Cot x)
Mathematics
(Subject)
(Common for Old & New Scheme)
( Session:- 2010-12 to 2013-15)
Paper: (I)
Time Allowed: 2.30 hours
(Inter Part – I)
Maximum Marks: 80
2. Answer briefly any Eight parts from the followings:
3. Answer briefly any Eight parts from the following:-
4. Answer briefly any Eight parts from the followings:-
Section-II
Attempt any three questions.
5. (a) Solve the system of linear equations by Crammer’s. Rule
2x+2y+z=3
3x-2y-2z=1
5x+y-3z=2
(b) Solve the system of equations 3x+2y=7 ; 3x2=25+2y2
6. (a) Resolve ![]() 3x+2y=7 ;3x2=25+2y2
3x+2y=7 ;3x2=25+2y2
(b) If the (positive) G.M. and H.M. between two numbers are 4 and ![]() , find the numbers
, find the numbers
7. (a) Find the values of n and r when n-1C r-1: nCr:n+1Cr+1 =3:6:11
(b) If x is very nearly equal 1, then prove that Pxp-qxq=(p-q)xp+q
8. (a) Prove that ![]() =
=![]()
(b) Find the values of the trigonometric functions of “-10350”
9. (a) Prove that r1+r2+r3-r = 4R
(b) Prove that tan-1![]() + tan-1
+ tan-1![]() - tan-1
- tan-1![]() =
=![]()