(A) A![]() B
B
(B) A ![]() B
B
(C) A![]() B
B
(D) B![]() A
A
Mathematics:A
Paper Code No.6191
Paper I (Objective Type)
(Inter-A-2015)
Time: 30 Minutes
Inter (Part I)
Marks: 20
Session (2011 - 2013 1(2012 - 2014) (2013. 13) (2014 - 16)
Note: Four possible choices A, B, C, and D to each question are given. Which choice is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.
Q.1
(A) ( 1 , 0 )
(B) (-1 , 0 )
(C) ( 0 , 1)
(D) ( 0 ,-1)
(A) A
B
(B) AB
(C) AB
(D) BA
(A) 2
(B) 3
(C) 4
(D) 6
(A) | A |
(B) K|A|
(C) K2 |A|
(D) K3|A|
(A) A-1
(B) A
(C)
(D) - A
(A) 0
(B) 1
(C) 2
(D) 3
(A) p +c
(B) -p + c
(C) p - c
(D) - (p + c)
(A)
(B)
(C)
(D)
(A) r<1
(B) |r|<1
(C) |r|=1
(D) |r|>1
(A) 0 < p (A)≤ 1
(B) 0 ≤P (A) ≤I
(C) 0 ≤P (A) < 1
(D) 0<P (A) < I
(A) P(A) +P(B)
(B) P (A) - P (B)
(C) P (A) • P (B)
(D) P (A) + P (B)-P (AB)
(A) 2n + 1
(B) 2n
(C) 2n + 2
(D) 3n + 1
(A) 10th, 11th
(B) 9th, 10th
(C) 11th, 12th
(D) 12th, 13th
(A)
+
(B)+
(C)+
(D)+
+
+
(A) 2
(B) π
(C)
(D) 2π
(A) Cos2α
(B) Sin2α
(C) Cos22α
(D) Sin22α
(A) [-1,1]
(B) [- 2, 2]
(C) (-1, 1)
(D) (- 2, 2)
(A)
(B)
(C)
(D)
(A)
(B)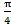
(C)
(D)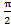
(A) 0
(B) 1
(C) 2
(D) Infinite
Time : 2 : 30 Hrs Marks : 80
Inter Part I
Mathematics
(Subjective)
Inter-A-2015
Session (2011-13)(2012.14)(2013-15)(2014-16)
Note: It is compulsory to attempt (8. 8 ) parts each from Q.No.2 and 3 While attempt any (9) parts from Q. No.4 and attempt any |(03) questions from Part II Write same Question No. and its Part No. as given in the question paper.(25x 2 = 50)
Q.2
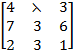
Q.3
Q.4
Part - II
5.(a) Prove that 05
|b+caa2|
|c+abb2| = (a+b+c)(a-b)(b-c)(c-a)
|a+bcc2|
(b) Show that Roots of x2 + ( mx + c )2 = a2 will be equal if C2 = a2 (1+m2): (5)
6.(a) Resolve ![]() into Partial Fractions.
into Partial Fractions.
(b) If y = ![]() x +
x +![]() x2 +
x2 +![]() x3 +------- and if 0 < x <
x3 +------- and if 0 < x < ![]() then show that x =
then show that x =![]()
7.(a) Find values of n and r when ncr = 35 and npr = 210
(b) Determine Middle Terms in the expansion (![]() x -
x -![]() )
)
8.(a) Prove that Cosθ + Sinθ ![]() +
+ ![]() =
= ![]()
(b) Show that Cot (α + β) = ![]()
9.(a) P and Q are two points in line with a tree. If the distance between P and Q is 30 m and the angles of elevation of the top of the tree at P and Q be 12° and 15° respectively, find the height of the tree. (5)
(b) Prove that Sin -1![]() + Sin -1
+ Sin -1 ![]() = Cos -1
= Cos -1 ![]()