Mathematics
Paper Code No. 81
Paper II (Objective Type)
Inter - A- 2015
Time Allowed : 30 Minutes
Inter (Part II)
Maximum Marks: 20
Session (2011 - 13) (2012 -14) (2013-15) (2014.16)
Note: Four possible choices A, B, C, and D to each question are given. Which choice is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.

• The output of a function is also called

(A) Result
(B) Domain
(C) Image
(D) None of these

(A)
(B)
(C)
(D)

• y = 5e^3x-4 then      =

(A) e^3x-4
(B) 15e^3x-4
(C) -5e^3x-4
(D) -15e^3x-4

(A) e²
(B) e⁸
(C) e⁶
(D) e⁴

•    [] =     

(A)  
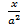
(B)  
(C)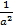  
(D) 

•  dx =

(A) tan
(B)
(C)
(D) tan-1        

• y= In (tanhx)  then  =

(A) Sech²xCothx
(B) 2Sechx
(C) SechxCoth²
(D) -2 SechxCothx

• The series X-+---------∞=

(A) Cosx
(B) Tanx
(C) Sinx
(D) -Sinx        

•  dx =

(A)
(B)
(C)
(D) Inx

•  =

(A) ln (ax+b)
(B) aln(ax+b)
(C)   in(ax+b)
(D) loga(ax+b)

• dx =

(A) 1
(B) ln2
(C) 2
(D) 3

•  dx =

(A) Sin^-1x
(B) Cos^-1x
(C) -Sin^-1x
(D) -Cos^-1x

• 2xdx =

(A)
(B)
(C)
(D)

• The point (-1,2) satisfies the inequality=         

(A) -y > 4
(B) x - y ≥ 4
(C) x + y < 4
(D) x + y > 4

• Equation of line parallel to x-axis =     

(A) x=0
(B) x= y
(C) y=a
(D) x=a

• P is mid point of  if P divides  in the ratio =    

(A) 1 : 1
(B) 2 : 2
(C) 1 : 2
(D) 2 : 1

• Equation of Circle with centre (0,0) and radius r =  

(A) x² + y² = r²
(B) x² - y² = r²
(C) x + y = r
(D) a - y = r

• If  α, β, π, are Direction Cosines of a vector then Cos2α+ Cos2β+cos2π  =

(A) 3
(B) 1
(C) 2
(D) 0

• (i x K)x J =          

(A) 1
(B) -J
(C) 0
(D) i

• The Parabola y² = 4ax, a > 0 opens =    

(A) Right Side
(B) Left Side
(C) Upward
(D) Downward

Mathematics
(Subjective)
Inter-A-2015
Inter Part - II
Time: 2: 30 Hours
Session (201113)(2012, 14)(2013 15)(2014.16)
Total Marks : 80
Note: It is compulsory to attempt (8. 8) parts each from Q.No.2 and 3 While attempt any (9) parts from Q. No.4 and attempt any |(03) questions from Part II Write same Question No. and its Part No. as given in the question paper.(25x 2 = 50)

Q.2

• Find the Domain and Range of =
• Evaluate Lim n+ ∞ (1+)n
• Differentiate Sin3x w.r.t Cos2x
• Find  if y =
• Find  if y = sin-1
• Find  if y =x2 in
• Find y2 if y =eax sinbx
• Find  if y3 3ax2 +x3 =0
• Verify f (f-1(x)) = x where x= (-x+9)3
• Write first three terms of f (x) =  x in Maclaurin Series.
• Determine the interval in which the function f(x) = x2 + 3x + 2, x(-4, 1) increases.
• If y= x4 + 2x2 + 2 then prove that  =4x

Q.3

• Use differentials to approximate the value of  .
• Evaluate
• Evaluate
• Evaluate 4xdx
• Evaluate dx
• Define Optimal Solution
• Evaluate   4xdx
• Find the area bounded by the curve y = x3 + 3x2 and the x-axis.
• Evaluate    dx
• Evaluate
• Define the Feasible Solution Set,
• Graph the Solution Set of Linear Inequalities in xy - Plane x + y ≥ 5 , - y + x ≤ 1      

 Q.4

• Find equation of Straight Line through (-4,7) parallel to 2x- 7y + 4 = 0 
• Find Horizontal and Vertical Lines through (-3, 7)
• Find distance of (6, -1) from line 6x - 4y + 9 = 0
• If Slope of l₁ =, Slope of l₂ =  find angle from l₁ to l₂
• Prove that the points A ( 3, 1 ) , B (-2 , -3) and C ( 2, 2 ) are vertices f an Isosceles Triangle.
• Find equation of Circle with ends of diameter at (-3,2 ) and (5,-6 )
• Write equation of tangent and normal to the circle x2 + y2 = 25 at (4,3)
• Find Focus and Vertex of Parabola x² = 4 (y -1).
• Find Centre and Foci of Hyperbola  -  =1
• Find a vector whose magnitude is 4 and is parallel to 2i - 3j + 6
• Find angle between vectors  = 2i - j + k - = - i + j
• Find a vector from point A to the origin where  = 4i-2j and B is (-2,5)
• Find the value of 2i x 2j.k

Part II

5. (a) Evaluate 
(b) If y = eax Sinbx then show that -2a + (a2+b2)y=0

6. (a) Find :  dx
(b) Find an equation of the perpendicular bisector of the segment joining the points A (3,5 ) and B ( 9,8)

7. (a) Evaluate dx
(b) Minimize f ( x , y ) = 3x + y ; subject to constraints 3x + 5y 15;   x + 6y ≥, 9;      x ≥0; y≥0

8. (a) Find the Coordinates of the point of intersection of the line.x + 2y = 6 with the circle x² + y² - 2x - 2y - 39 = 0
(b) Prove that Cos (α- β) = CosαCosβ + Sin α Sinβ  

9. (a) Find the Focus, Vertex and the Directrix of the Parabola ( x - 1 )2 = 8 ( y + 2 )
(b) Find the area of the triangle determined by P, Q, R P (1, - 1, - 1),Q (2, 0,-1), R (0, 2, 1)