D.G KHAN
BOARD2015
Inter Part I
Mathematics
Group I
NOTE: You have four choices for each objective type question as .A , B , C and D . The choice which you think is correct, fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.
Q.1:
- The multiplicative identity of real numbers is:
(A) 0
(B)
1
(C)
2
(D)
3
- If A is a subset of B then complement of A in B is A° =
(A) A-B
(B)
B-A
(C)
A∩B
(D)
A∪B
- If A=
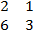 then cofactor of 6 is:
then cofactor of 6 is:
(A) + 1
(B)
-1
(C)
-6
(D)
3
- If AB exist then (AB)-1 =
(A) (A-1)(B-1)
(B)
(B-1)(A-1)
(C) 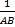
(D) 
- Which of the following is unary operation?
(A) Addition
(B)
Multiplication
(C)
Square root
(D)
Division
- The degree of polynomial √ax5+ bx4 + cx3 =5 is:
(A) 
(B)
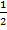
(C)
5
(D)
2
- The roots of equation ax2+bx+c=0 are rational if:
(A) b2-4ac >0
(B)
b2-4ac=0
(C)
b24ac<0
(D)
None
- Partial fractions of
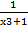 will be of the form:
will be of the form:
(A) 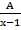 +
+ 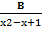
(B)
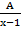 +
+ 
(C)
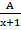 -
- 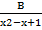
(D)
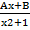 +
+ 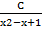
- The arithmetic mean between 2+
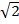 and 2-
and 2- is:
is:
(A) 2
(B) 
(C)
0
(D)
4
- if nth term of an A.P is
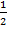 (3-n) the first two terms are:
(3-n) the first two terms are:
(A) 1,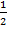
(B)
2,
(C)
3,1
(D) 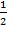 ,
,
(A) 6
(B)
4
(C)
5
(D)
8
- If n(S) =20; n(B) =20 then P(B):
(A) 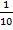
(B)
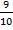
(C)
10
(D) 
- Expression of (3-5x)1/2 is valid if:
(A) |x| <5
(B)
|x|< 
(C)
|x| < 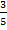
(D)
|x| < 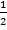
- The coefficient of last term n the expansion of (a+b)5 is:
(A) 1
(B)
-1
(C)
0
(D)
5
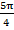 radian =
radian =
(A) 360°
(B) 335°
(C)
270°
(D)
225°
- Sin (α-
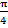 ) =
) =
(A) Sec α
(B)
-Cos α
(C)
Cos α
(D)
-Sin α
(A) [-1,1]
(B)
[-1,0]
(C)
[ 0, 2]
(D)
[-2, 2]
- tan
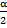 =
=
(A)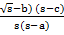
(B)
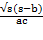
(C)
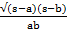
(D)
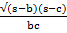
(A) -Cos-1 x
(B)
Cos-1 x
(C)
π- Cos-1 x
(D) 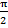 -Cos -1 x
-Cos -1 x
- Reference angle of tanθ =-1 equals:
(A) 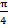
(B)
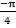
(C)
-π
(D)
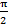
SUBJECTIVE TYPE
SECTION-I
Q.2.Attempt any 8 short questions:
- Find multiplicative inverse of (√2, √5)
- Find the modulus of l-I √3
- Prepare a table of addition of the element of the residue classes modulo 4
- Construct the truth table of (P~P) → q
- Define semi- group
- For A= {1,2,3,4,5}. Find the relation {(x,y)|x+y<5} in A
- Define diagonal matrix
- If A=
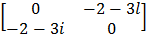 , show that A is Skew Hermitian.
, show that A is Skew Hermitian.
- If A=
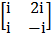 , B=
, B= 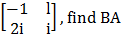
- A number exceeds its square root by 56. Find the number.
- Evaluate (-1 + √-3)5 + (1- √-3)5
- State the remainder theorem.
Q.3.Attempt any 8 short questions:
- Resolve
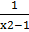 into partial fractions:
into partial fractions:
- Write the next two terms of -1,2,12,40...
- Define Arithmetic mean.
- Insert two geometric means between 1 and 8
- Write usual prove that G2 = A x H
- Find the value of n when nP2 = 30
- Define a combination and permutation?
- What is the Probability that a slip of number divisible by 4 are picked from the slips bearing numbers 1,2,3………10
- Check, 1+2+4 ……… +2n-1 =2n -1 for n=1, 2
- Use Binominal theorem to Evaluate (9.9)5
- Expand up to four terms (1+2x)-1
Q.4. Attempt any 9 questions:
- Find r, when l=5 Cm, θ =
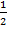 radian
radian
- If α, β, γ are the angles of ∆ABC then prove that Sin (α + β) = Sin γ
- Without using table find S.n 45°
- Prove that cos(θ-180 °) = -Cos θ
- Prove Cot α- tan α =2Cot 2 α
- Find the period of Cosec 0x
- Show that r= (s-a) tan
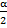
- Define the in- circle
- Solve the ∆ABC if β=60° , γ=15°, b= √6
- Find the values of Cos-1 (1)
- Find the value of Cos(Sin-1
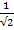 )
)
- Solve Cosecθ =2
- Solve Cot2 θ=

SECTION-II
Attempt any three questions from this section:
5.(a) 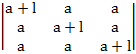 = l2 (3a+ l)
= l2 (3a+ l)
(b) Solve the equation (x-  ) 2 + 3(x+
) 2 + 3(x+ ) =0
) =0
6.(a) Resolve 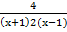
(b) Find ‘n’ so that 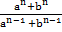
7.(a) Prove that n-1Cr + n-1 Cr-1 = n Cr
(b) Find the coefficient of xn in the expression of 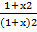
8.(a) If cosec θ = 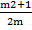 and m>0, (0< θ<
and m>0, (0< θ<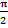 ) find the values of the remaining trigonometric ratio
) find the values of the remaining trigonometric ratio
(b) Prove that 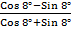 = tan 37°
= tan 37°
9.(a) Prove that abc (Sin α+ Sin β + Sin γ) = 4 ∆ S
(b) Prove that Sin -1  + Sin -1
+ Sin -1  = Cos -1
= Cos -1 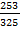
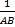
+
+
-
+
,
-Cos -1 x
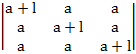 = l2 (3a+ l)
= l2 (3a+ l)![]() ) 2 + 3(x+
) 2 + 3(x+![]() ) =0
) =0![]()
![]()
![]()
![]() and m>0, (0< θ<
and m>0, (0< θ<![]() ) find the values of the remaining trigonometric ratio
) find the values of the remaining trigonometric ratio ![]() = tan 37°
= tan 37° ![]() + Sin -1
+ Sin -1 ![]() = Cos -1
= Cos -1 ![]()