D.G KHAN BOARD-2015
Inter Part II
Mathematics
Group I
NOTE: You have four choices for each objective type question as .A , B , C and D . The choice which you think is correct, fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.
Q.No.1
(a) (-∞,∞)
(b) (-∞,0)
(c) (0,∞)
(d) (-1, 0)
(a) 1
(b)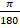
(c) -1
(d)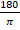
(a)
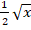
(b)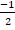
(c)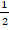
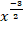
(d)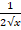
(a) Cos x
(b) 1
(c) 0
(d) -1
(a)
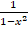
(b)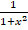
(c) tan x
(d) Sec x
(a) 4 eax
(b) 2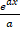
(c) 3eax
(d) xeax
(a)ax
(b) axx-1
(c) xeax
(d)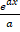
(a) eax
(b) aeax
(c) xeax
(d)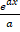
(a) 0
(b) 2
(c) -2
(d) 1
(a) Sec x tan 2 x
(b)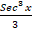
(c)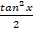
(d)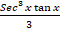
(a)
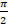
(b)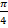
(c) 1
(d) 0
(a) ln(ln x)
(b) x
(c)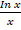
(d)
(a) y= Ce-x
(b) Ce x
(c) e cx
(d) xe –x
(a) 2
(b)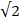
(c) 1
(d)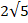
(a) 2: 1
(b) 1: 2
(c) 1: 3
(d) 3: 1
(a) Upper and lower half planes
(b) Upper and right half planes
(c) Left and right half planes
(d) Left and lower half plane
(a) r = 1
(b) r = 2
(c) r = -1
(d) r = 0
(a) Circle
(b) Parabola
(c) Hyperbola
(d) Ellipse
(a) 0
(b) 1
(c) -1
(d) 2
(a) 0
(b) 1
(c) 2
(d) -1
SUBJECTIVE TYPE:
3. Attempt any eight short questions:
4. Attempt any 9 short questions: (18)
Attempt any three questions from this section:
5. (a) If f(x) = ![]()
![]() ; x ≠ 2 find k so that f(x) is continuous at x=2;
; x ≠ 2 find k so that f(x) is continuous at x=2;
(b) Differentiate ![]() w.r.t x3
w.r.t x3
6. (a) Evaluate ![]() dx
dx
(b) One vertex of a parallelogram s (1,4), the diagonals intersect at (2, 1) and the sides has slope 1 and -1/7. Find other three vertices.
7.(a) Solve the different equation y-x ![]() =2 (y2+
=2 (y2+![]() )
)
(b) Maximize the function defined by f(x,y) =2x+ 3y subject to the constraints
2x+y ≤8 , x+2y ≤ 4, x ≥0, y ≥ 0
8. (a) Find an equation of the circle passing through the point A(1,2) and B(1, -2) and touching the line x+2y+5=0
(b) By vector method, prove that Cos(α+β)=Cos α Cos β – Sin α Sin β
9. (a) A parabolic arch has a 100m base and height 25m. Find the height of the arch at the point 30m from the centre of these.
(b) If a + b + c = 0 then prove that a x b = b x c = c x a
D.G KHAN BOARD-2015
Inter Part II
Mathematics
Group II
NOTE: You have four choices for each objective type question as .A , B , C and D . The choice which you think is correct, fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.
Q.No:1
(A) {1}
(B) {-1,1}
(C) {-1}
(D) R-{-1,1}
(A) Constant function
(B) Even function
(C) Odd function
(D) Neither even nor odd
(A) cos x
(B) -x
(C) -sin x
(D) x
(A) Sy/sx
(B) Sx/sy
(C) Dy/dx
(D) Dx/dy
(A) 1
(B) 0
(C) -1
(D) ∞
(A) -4
(B) 4
(C) ¼
(D) -1/4
(A)
(B) Secx tanx
(C) cos 2x cosec x
(D) -cos 2x cosec x
(A) a x + c
(B)
(C) lnax + c
(D) lna ax + c
(A) 1
(B) 0
(C) Constant
(D) x
(A) 1/x
-2y=0
(B) x-2 =0
(C)-2y=0
(D)
(A) 0
(B) 2
(C) -2
(D) 1
(A) cosy = cosx +c
(B) y = x+c
(C) cosy = cosy+ c
(D) -Cosy= -Cosy + c
(A) ecos x + c
(B) sin x ecos x + c
(C) e sinx + c
(D) e sinx cos x + c
(A) ½
(B) 2
(C) 3
(D) 1/3
(A) Line is parallel to y-axis
(B) Line is parallel to x-axis
(C) Line passes through origin
(D) Line is perpendicular
(A) 2x+3>0
(B) x +4>0
(C) x+ 5 >0
(D) 2x + 3 <0
(A) X+2
(B) Y+2
(C) X-a
(D) Y-a
(A) X=0
(B) Y=0
(C) Fx+ gy=0
(D) Gx+fy=0
(A) 1,0,0
(B) 1,0,1
(C) 1,1,0
(D) 0,0,1
(A) F x CP
(B) CP x F
(C) CP x F
(D) OP x F
SUBJECTIVE TYPE
2. Attempt any 8 questions: (16)
3. Attempt any eight short questions:
4. Attempt any nine short questions:
Attempt any three questions from this section:
5. (a) Evaluate ![]()
(b) If y = tan (2tan -1 x/2), show that dy/dx =4 ![]()
6. (a) Solve 2 ex tany dx + (1-ex) Sec2y dy =0
(b) If two lines with slopes m1 and m2 are perpendicular, then prove that m1.m2=-1
7. (a) Evaluate ![]()
(b) Maximize the function f(x,y) = 2x +3y subject to the constraints:
2x+y ≤8
x+2y≤14
x≥0 ; y≥0
8. (a) Write equation of circle which pass through A(4,5), B(-4,-3), C(8,-3)
(b) prove that in any triangle ABC, b=c CosA + aCosC
9. (a) Find the focus, vertex and directrix of the parabola x+8 –y2 +2y=0
(b) A force of magnitude 6 units acting parallel to 2i + 2j + k displaces the point of application from (1,2,3) to (5,3,7). Find the work done.