Inter (Part-I) Dera Ghazi Khan Board 2015
Statistics
Part I (Objective Type)
Time Allowed: 20 Minutes
Max. Marks: 17
Note: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.
Question #1
Circle the correct option i.e. A/B/C/D. Each part carries one mark.
(A) On the average
(B) Always
(C) In the long run
(D) A and C
(A) Histogram
(B) Frequency polygon.
(C) Ogive
(D) None of these
(A) Frequency distribution
(B) classification
(C) Tabulation
(D) Array
(A) 0
(B) 1
(C) 2
(D) 3
(A) A.M
(B) G.M
(C) Made
(D) Median
(A) Never
(B) Always
(C) Sometimes
(D) Often
(A) 25
(B) 125
(C) 5
(D) 0
(A) b2 > 3
(B) b2 < 2
(C) b2 = 3
(D) b1 > 3
(A)
(B)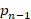
(C)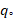
(D)
(A) Fixed
(B) Changed
(C) Constant
(D) None Of These
(A) 6
(B) 2
(C) 36
(D) 12
(A) Zero
(B) 1
(C) 0.5
(D) 0.8
(A) P(x = x)
(B) P(xx)
(C) P(xx)
(D) None of these
(A) Mean
(B) Variance
(C) S.D
(D) Co-variance
(A) x and n
(B) x and p
(C) n and p
(D) x, n and p
(A) Zero to ∞
(B) zero to n
(C) -1 to ∞
(D) Undefined
(A) 2
(B) 3
(C) 1
(D) 4
Inter (Part-I) Dera Ghazi Khan Board 2015
Statistics
Part I (Subjective)
Time Allowed: 2.10 Hours
Max. Marks: 83
Section I
2. Write short answers any Eight (8) questions of the following
3. Write short answers any Eight (8) questions of the following
QUESTION NO.4 Write short answers any Six (6) questions of the following
(1) What is mathematical expectation?
(2) Given E(x) = 2.5 and Var(x) - 1.2: find E (![]() )
)
(3) If E(x) = 10, then find E(5x -25)
(4) What is random Experiment?
(5) Write down the properties of discrete probability distribution
(6) Write down two properties of Binomial experiment
(7) If n= 5 and P=0.3, then find standard deviation of a Binomial distribution
(8) Given for hyper geometric. Distribution N =10; n = 2 and K = 2, Find P(x = 0)
(9) Write mean and variance of Hyper geometric distribution
SECTION - II
Note: Attempt any three questions from this section
Question #5
(a) Find the H,M for the data given below
| X | 10 | 11 | 14 | 16 | 18 | 20 |
| f | 1 | 3 | 7 | 12 | 8 | 1 |
(b) Compute Mode from the following data
| Classes | 2 - 4 | 4 - 6 | 6 - 8 | 8 - 10 | 10 - 12 |
| Frequecy | 4 | 10 | 15 | 12 | 3 |
Question #6
(a) Find mean deviation from the following data
| x | 21 | 22 | 23 | 24 | 25 |
| f | 3 | 8 | 9 | 7 | 6 |
(b) The first four moments about x = I.5 c f a variable are 1, 17, 10 and 40 find variance ![]()
Question #7
(a) Find Laspeyr’s index number taking 1980 as base
Commodity |
Prices |
Quantities |
|
1980 1981 |
1980 1981 |
A |
2 6 |
50 40 |
B |
4 8 |
60 30 |
C |
6 10 |
40 10 |
(b) If P(A)=![]() ,P (A
,P (A![]() B)=
B)=![]() B) P(
B) P(![]() =
= ![]() then find (i) P(A
then find (i) P(A ![]() B) (ii) P(
B) (ii) P(![]() B) (iii) P(
B) (iii) P(![]() ) (iv) P(
) (iv) P(![]() )
)
Question #8
(a) Let x be a random variable with Prab distribution
| x | -3 | -2 | 2 | 3 | 4 |
| P(x) | 2/10 | 1/10 | 1/10 | 2/10 | 4/10 |
(b) A continuous random variable x has probability function f(x) = Cx for 0 < x <2 Determine (i) c value P(I < x < 1.5) (ii) P(I![]() x < 1.5) (iii) P(x < 1.5)
x < 1.5) (iii) P(x < 1.5)
Question #9
(a) Out of 10-applicants for a job, 6 are from Lahore. If 3 applicants are selected at random, find the probability that (a) 3 are from Lahore (b) At least 2 are from Lahore
(b) Find the Mean and SD of the binominal (q + P)3
SECTION – (III)
Question #10
Attempt any three parts from A B, C and D 5x3 15
(A) The following is the frequency distribution of number of leaves on branches of a tree, Find Mean, median and modal number of leaves per branch
| No. Of Leaves | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| No. Of branches | 3 | 8 | 11 | 18 | 20 | 13 | 9 | 5 |
(B) Calculate mean deviation from median for the following frequency distribution
| Groups | 10 - 14 | 15 - 19 | 20 - 24 | 25 - 29 | 30 - 34 | 35 - 39 |
| Frequecy | 2 | 4 | 6 | 12 | 5 | 1 |
(C) Compute index number by simple aggregative method taking 2000 as base for the following data
Items |
Prices |
Quantities |
|
2000 2001 2002 |
2003 2004 |
Wheat |
20 25 30 |
32 35 |
Rice |
40 50 60 |
65 70 |
Cotton |
60 65 70 |
80 90 |
(D) For the following probability distribution
| X | 0 | 1 | 2 | 3 | 4 |
| P | 15/210 | 80/210 | 90/210 | 24/210 | 1/210 |
Calculate (i) E(x) and E(![]() ) (ii) Show that E(2x + 5) =2E(x) + 5
) (ii) Show that E(2x + 5) =2E(x) + 5
(E) A committee of size 6 is to be selected at random from 8 women and 7 men. Find the probability distribution of number of women in the committee