FAISALABAD BOARD 2015
PAPER MATHEMATICS
PART-I
Time: 30 Min
Marks: 20
Note: Four Answers are given against each column A,B,C&D. Select the write answer and only separet answer sheet, fill the circle A,B,C or D with pen or marker in front of that question number.

Question#1

• If n is prime number, Then 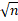 is:
  
  (a) Natural number     
  (b) Integers
  (c) Rational number    
  (d) Irrational number
  
  
• Set of integers is a group with respect to:
   
  (a) +
  (b) ÷
  (c) x                
  (d) -
  
  
• Tabular form of {χ|χ∈ p ˄ χ >12}
  
  (a) {1, 2, 3, 5, 7, 11}
  (b) {2, 3, 5, 7, 9, 11}
  (c) {2, 3, 7, 11}
  (d) {2, 3, 5, 7, 11}
  
  
• The cofactor of an element aμ denoted by Aμ:
  
  (a) (-1)μ Mij
  (b) (-1)1-j Mij
  (c) (-1)1+j Mij
  (d) (1)1+j Mij
  
  
• If A and B are non-singular matrices, then (AB)^-1 =:
  (a)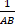   
  (b) B^-1A^-1
  (c) A^-1B^-1
  (d) AB
  
  
• An equation 16(x4 +1)- 8(x3 + x)+ 9x2 =0 is of the form:
  
  (a) Exponential           
  (b) Radical
  (c) Rational     
  (d) Reciprocal
  
  
• If ω is the imaginary cube roots of unity then 
  
  (a) ω
  (b) ω^-1
  (c)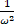   
  (d) ω³
  
• Partial fraction of 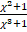 is:
  
  (a)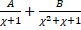           
  (b)
  (c)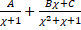
  (d)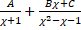       
      
  
• If A, G and H are arithmetic, goemetric and harmonic Means, then
  
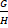
  (a) A/G   
  (b) G/A
  (c) H/G
  (d) G2
  
  
• If a, A, b are in A.P., then 2A=:
  
  (a) (a+b)/2   
  (b) a + b          
  (c) 2(a + b)      
  (d) a - b
  
  
• When P(A∩B) = P(A)P(B) then A and B are events 
  
  (a) Mutually exclusive
  (b) Equally likely
  (c) Independent
  (b) Dependent 
  
• n Cn=      
     
  (a) 0
  (b) 1
  (c) n    
  (d) n!
  
  
• Sum of coefficient in the expansion of (1+x)5 is:
  
  (a) 8    
  (b) 16  
  (c) 32  
  (d) 64
  
  
• Cos2 3θ+ sin2 3θ=:
  
  (a) 1    
  (b) 2    
  (c) 3    
  (d) 4
  
  
• 2nd term in (1-x)-r is:
  
  (a) 1
  (b) x
  (c) 2x
  (d) 3x
  
  
• sin 2a
  
  (a)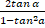   
  (b)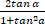       
  (c)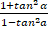       
  (d)       
  
  
• Rang of sin X is    
  
  (a) (-1 ,1)        
  (b) ( -1, 1)       
  (c)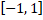        
  (d) (-1, 1]
  
  lf a= 90° then:
  
  (a) c² = a² + b²
  (b) b² = a² + c²
  (c) c² = b² + c² 
  (d) a² = b² + c²
  
  19. tan (tan^-1(1))=.
  
  (a) 1    
  (b)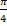
  (c)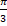  
  (d) 0
  
  
• sin x =  then x is:
  
  (a) π/6,5π/6
  (b) π/3,5π/3
  (c) π/6,π/3/
  (d) π/3,&5π/6
  

Time: 2:30 Hours
(Subjective Part)
SECTION-I

2.  Attempt any Eight Parts, 16

• Separate real and imaginary parts of :
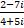
• Find multiplicative inverse of -3 -5i.
• Define complement of a set.
• Write the converse and inverse of ~ p →q.
• For A = (I, 2, 3, 4), find the relation
  
• If a,b are elements of a group G, then show that (ab)^-1=b^-1 a^-1
• find X and y if
  
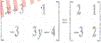
• lf A and B are matrices of same order, then explain why in general 
  
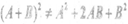
• Show that a
  
   
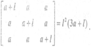
• Evalutate, (1+ω-ω²)(1-ω+ω²)
•  If a,β are the roots of 3x2 - 2x+4= 0, then and the value of
• When x⁴ + 2x³ + kx² + 3 is divided by x - 2, the remainder is 1. Find the value of k.
  

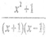
3. Attempt any Eight Parts,16

• Resolve x²+1/(x+1)(x-1) in to partial fractions
• If a_n-2=3_n-11 , find nth terms of sequence
  
  
• Find A.M. between 1 – x+x² and 1+ x+ x².
  
  
• Find the 5th term of G.P.3,6,12,…..
• Find nth term of H.P,1/2,1/5,1/8,......
• Evaluate:
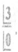
• Find the value of n when ¹¹ P_n=11.10.9 .
• Evaluate: ¹¹C₄.
• Determine the probaility of getting 2 heads in two successive tosses of a balanced coin.
• Show that 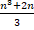 represent an integer for n = 1,2.
• Calculate by means of binomial theorem (2.02)⁴
• Expand up to 4 terms

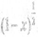
4. Attempt any Eight Parts, 16

• Prove that
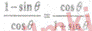
• Prove that sec²θ-cosec²θ= tan²θ- cot²θ
• If a,β, 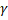 are angles of a triangle ABC then prove that tan (a +β)+ tan 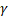=0
• Show that cos (a + β)cos (a- β)= cos²β –sin² a,
• Prove that cot a- tan a = 2 cot 2a .
• Express sin 5x + sin 7 x as a product.
• Find the period of cosec 10x.
• Find the smallest angle of the triangle ABC when a = 37.34, b 3.24, c = 35.06.
• Find the area of the triangle ABC when a = 200, b =12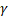0,  =150°
• Find r² of the triangle ABC, when a = 34, b = 20, c 42.
• Without using calculator, show that cos^-1  cot^-1 . 
• Find the solution of sin x = 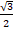 which lies in [0,2π] 
• Solve: sec²θ =4/3 in [0,2π] 

SECTION-II

10. Attempt any THREE question each question carries 10 marks
Question#5
(a) Use Cramer's rule to solve the system.
(b) If a,β are the roots of x2-3x+5=0 form the equation whose roots are 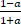 and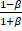

Question#6
(a) Resolve into partial fractions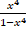
(b) Show that the sum of n A.Ms between a and b is equal to n times their A.M.

Question#7
(a) Show that ¹⁶C₁₁+ ¹⁶C₁₀=¹⁷C₁₁
(b) Find the term independent of x in the expression of 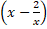10

Question#8
(a) Prove that 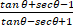= tanθ+secθ
(b) If sin a =  and cos β =  where 0 < a < 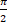 and 0 < β  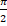<  show that sin(a - β )= .

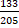Question#9
(a) Prove that
(b) Prove that