Inter (Part-II) Faisalabad Board 2015
Mathematics
Part II (Objective Type)
Time Allowed: 30 Minutes
Max. Marks: 20
Note: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.
Question #1
Circle the correct option i.e. A/B/C/D. Each part carries one mark.
(a) sin-1

(b) sin-1
(c) sin-1
(d) sin-1
(a)
(b)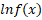
(c)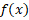
(d)
(a)
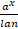
(b) ax
(c)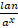
(d) axlan
(a) cosh-1x
(b) sinh-1x
(c) tanh-1x
(d) sech-1x
(a) 1
(b) -1
(c) 0
(d) None
(a)
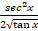
(b) sec2 x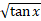
(c)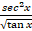
(d)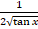
(a) ex
(b)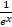
(c) 1
(d) ex-1
(a) ecos x
(b) esin x
(c) e-sin x
(d) –sin xecos x
(a) Even
(b) odd
(c) Both even and odd
(d) Neither even nor odd
(a) 0
(b) 2a
(c) a2
(d) Undefined
(a) 0
(b)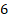
(c) -6
(d) None
(a)
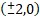
(b)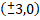
(c)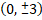
(d)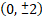
(a) (7,6)
(b) (-7, -6)
(c) (-14, -12)
(d)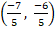
(a) x + y < 2
(b) x + y < 0
(c) x - y < 2
(d) x - y > 0
(a) a + b > 0
(b) a + b = 0
(c) h2-ab<0
(d) h2 – ab = 0
(a) y = x
(b) y = -x
(c) y =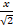
(d) y = mx
(a) 0
(b) 1
(c) -2
(d) 2
(a) 0
(b) x
(c)
(d)
(a) ex
(b) xex
(c) ex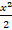
(d) None
(a) 0
(b) π
(c)
(d)
Inter (Part-II) Faisalabad Board 2015
Mathematics
Part II(Subjective)
Time Allowed: 2.30 Hours
Max. Marks: 80
Section I
2. Attempt any Eight Parts
3. Attempt any Eight Parts
4. Attempt any Nine Parts (18)
(Subjective Part)
SECTION-II
Question #6
(a) Evaluate ![]()
(b) Find the equation of line passing through the point of intersection of lines x-y-4 = 0and 7x + y + 20= 0 and perpendicular to line 6x + y - 14 = 0.
Question #7
(a) Evaluate ![]() .
.
(b) Graph the fesible region and find the corner points for the following system of inequalities subject to constraint:
x- y ![]() 3 ; x + 2y
3 ; x + 2y ![]() 6
6 ![]()
Question #8
(a) Find equation of tangent to circle x2 +y2 =2 and perpendicular to line 3x+ 2y =6.
(b) Prove that angle in a semi circle is a right angle.
Question #9
(a) Find focus, vertex and directrix line of the parabola x2 = 5y
(b) Find the value of a so that ai +j, +3k and 2i + j – 2k are coplanar