Statistics (New Scheme)
Gujranwala Board 2015
Inter Part II
Time:20 Minutes
Objective Type
Max. Marks: 17

Note: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct, fill that circle in front of that question number with marker or pen on the answer book provide. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank.

Question#1

• Normal curve always --------------
  
  (a) stays above x-axis
  (b) touches x-axis
  (c) goes below x-axis
  (d) none
  
  
• The two points containing the middle 68.27 % area under a normal curve are:
  
  (a) µ ± 2 ά
  (b) µ ± ά
  (c) µ ± 3 ά
  (d) none
  
  
• In a normal distribution ß1 = 0 and ß2 = --------------
  
  (a) 3
  (b) less than 3
  (c) greater than 3
  (d) none
  
  
• The collection of information from a part of population is called:
  
  (a) sample survey 
  (b) census
  (c) population
  (d) none
  
  
• The process of dividing a heterogeneous population into homogeneous subgroups is called:
  
  (a) stratification 
  (b) sampling
  (c) ranking
  (d) none
  
  
• Bias is -----------
  
  (a) decreasing
  (b) de-cumulative
  (c) cumulative
  (d) none
  
  
• Population parameters are estimated from -------------
  
  (a) sample data
  (b) population data
  (c) census data
  (d) none
  
  
• By decreasing 'n', the length of the confidence interval for µ.
  
  (a) decreases
  (b) no effect
  (c) increases
  (d) none
  
  
• If µ ≠60, then test is called:
  
  (a) one tailed
  (b) two tailed
  (c) A and B
  (d) none
  
  
• The best fitting curve has sum of squares of residuals:
  
  (a) Maximum
  (b) Minimum
  (c) Largest
  (d) None
  
  
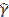• For  =a + bx, Σ(y-) is always
  
  (a) Equal to zero
  (b) Negative
  (c) Greater than zero  
  (d) None
  
  
• The value of correlation co-efficient is always in the range:
  
  (a) 0 to 1
  (b) -1 to 0
  (c) -1 to 1
  (d) All
  
  
• In the study of attributes, no class frequency can be ------------
  
  (a) Positive
  (b) Negative
  (c) Greater than zero
  (d) None
  
  
• Two attributes A and B are independent if (AB) = -------------
  
  (a)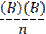
  (b)
  (c)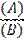
  (d)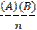
  
  
• A time series is function of -------------
  
  (a) Groups
  (b) Frequency
  (c) Time
  (d) None
  
  
• The lowest point relative to the-rest of the particular cycle Is -----------
  
  (a) Trough
  (b) Peak 
  (c) Expansion
  (d) None
  
  
• ALU stand for --------------
  (a) arithmetic logical unit  
  (b) all logical units
  (c) alone logical unit
  (d) none

Statistics (New Scheme)
Gujranwala Board 2015 
Inter Part II
Time:3:10 Hour
Subjective Type
Paper II
Max. Marks. 83
Note: Section I is compulsory. Attempt any three (3) questions from Section II and any three (3) parts form Section III.
(SECTION-I)

2. Write short answers to any EIGHT questions: (2x8=16)

• In a normal distribution µ2= 16, find the value of µ4.
  
• In a normal distribution σ²= 15, fine the values of ß and ß2.
  
• In a normal distribution Q1 = 8, Q3 = 17, find the values of mean and mode.
  
• Write down any two properties of normal distribution.
  
• Write the equation of standard normal distribution.
  
• What is meant by teast of hypothesis?
  
• Define point estimation and interval estimation.
  
• Define level of significance and level of confidence.
  
• Find the value of‘t’ if n = 20, x = 4, S = 3 and µ = 4,
  
• What is meant by simple and composite hypotheses?
  
• What is computer?
  
• What is compiler?

3. Write short answers to any Eight questions: (2x8=16)

• Define sampled population.
  
• What do you mean by probability sampling?
  
• Explain Quota sampling.
  
• Define statistic.
  
• Describe. Bias.
  
• Define sample design.
  
• Explain what is regression.
  
• Define independent variable.
  
• Describe regression co-efficient.
  
• Define negative correlation.
  
• Write two properties of correlation co-efficient.
  
• Give that bxy = -16.6, byx = -0.4, find r.

4. Write short answers to any SIX questions: (2x8=16)

• Define rank correlation.
  
• Differentiate between attribute and variable.
  
• Define co-efficient of contingency.
  
• Write the normal equations of straight line.
  
• What is secular trend?
  
• Describe the semi - average method.
  
• Write the additive model of time series.
  
• Give two examples of random variations.
  
• Define signal and noise.

(Section-II)

Question#5
(a) Let X ~ N (20, 25), find the area under the normal curve between 30 and 42. 4
(b) In a normal distribution µ = 30, σ = 5. Find two points containing middle 90% area. 4

Question#6
(a) Draw all possible samples of size 2 with replacement from the population 1, 3, 5. Show that. 4 

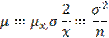
(b) A population consists of values 4, 6, 1 12, 18 and 20. If samples of size 2 ate drawn without replacement, then compute µẍ and  σ 2/x  without drawing samples. 4

Question#6
(a) A sample poll of 100 voters chosen at random from all voters in a given district indicated that 55% of them were in favor of a particular condidate. Find 95% confidence limits for the proportion of all the voters in favour of this candidate,
(b) A random sample of 36 drinks from a soft drink machine has an average content 7.6 ounces with a standard deviation of 0.48 ounces. Test the hypothesis Ho:µ≤7.5 ounces against the alternative hypothesis HI : µ7.5 ounces at the 0.05 level of significance. 4

Question#8
(a) Compute the regression coefficients in the following case N = 10, Σ(x-ẍ)² = 170, Σ(yi-y)²= 140, Σ(x-x)(yi-y) = 92
(b) For a set of 20 pairs of observations we have x= 2, y=8,
Σx²_i=180, Σy²_i=3424, Ex_iy_i=604, Compute correlation coefficient.4

Question#9
Q9. (a) Find the spearman's rank correlation coefficient for the following data: 4

(b) For the following data calculate 3- ears moving averages.4 

SECTION-III
(PRACTICAL)

Question#1
(A) There are six digits in a population i.e., 2,4,5,7,10,11. Draw all possible samples of size 3 without replacement and find the sample proportion  of prime numbers in each sample. Verify that    =
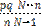
(B) Samples of size 10 and 15 respectively are drawn from different population with the same unknown standard deviation. The means and biased variances of the sample are
     X₁ = 20, X₂ = I5, S²₁ = 16, S²₂ = 14. Is the difference between means significant? 5 
(C) From the following table, fit a simple linear regression line Y on X.

(D) For the data given below determined whether the two attributes are independent positively associated or negatively associated.5
(i) N =1024 (A) =144 (B) = 384 (AB) = 54
(ii) N = 1000 (A) = 400 (AB). 200 (αβ) = 50
(iii) (AB) = 70 (Aß) =10 (αB) = 30 (αβ) =140
(E) Calculate 7 year moving average for the following data: 5