Mathematics
Inter Part-II
Group - I
Lahore Board 2015
Time: 30 Min.
Objective Type
Marks = 20
Note: Four possible answers A, B, C and D to each question are given. The choice which you think is correct, fill that circle in front of that question with Marker or Pen ink in the answer-book. Cutting or filling two or more circles will result in zero mark in that question.
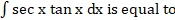 :
:
(A) tan x
(B) sec2x
(C) tan2 x
(D) sec x
- The point of intersection of medians of a triangle is called :
(A) Centroid
(B) Orthocentre
(C) Circumcentre
(D) Incentre
- The parabola x2 = y passes through point :
(A) 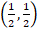
(B) 
(C) 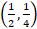
(D)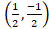
- The distance of point P (6, -1) from the line 6x - 4y + 9 =0 is:
(A)49
(B) 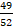
(C) 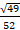
(D)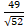
- The integration is the reverse process of :
(A) Induction
(B) Differentiation
(C) Tabulation
(D) Sublimation
- (1, 0) is the solution of inequality:
(A) 7x + 2y < 8
(B) x - 3y < 0
(C) 3x + 5y < 6
(D) -3x + 5y > 2
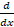 (sin-1x) is equal to:
(sin-1x) is equal to:
(A) 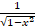 1
1
(B)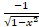
(C)
(D)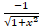
- If f(x)=x2- x then f(-2) is equal to :
(A) 2
(B) 6
(C) 0
(D) -6
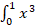 dx is equal to :
dx is equal to :
(A) 4
(B) -4
(C)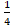
(D)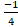
- Solution of differential equation,
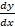 - y is :
- y is :
(A) cex
(B) ce-x
(C) ex
(D) e-x
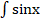 dx is equal to :
dx is equal to :
(A) cos x
(B) sin x
(C) -sin x
(D) - cos x
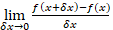 is equal to:
is equal to:
(A) f (0)
(B) f ' (a)
(C) f ' (x)
(D) f ' (0)
- If f (x) = eax then f '(x) is equal to:
(A)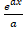
(B) 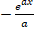
(C) 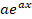
(D) 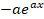
- If f (x) = cos x then f (0) is equal to:
(A) 0
(B) -1
(C) 1
(D)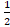
- A vector with magnitude 1 is called :
(A) Null vector
(B) Unit vector
(C) Zero vector
(D) Constant vector
- The set of all points in the plane that are equally distant from a fixed point is called:
(A)Ellipse
(B) Parabola
(C)Hyperbola
(D) Circle
(A) 0
(B) -1
(C) 1
(D) 2
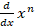 is equal to
is equal to
(A) 
(B) 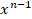
(C)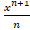
(D)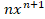
(A) 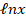
(B) 
(C) 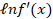
(D) f(x)
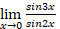 is equal to
is equal to
(A) 
(B) 
(C)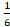
(D)
Mathematics
Lahore Board 2015
Time: 2.30 hrs
Essay Type
Inter-II
Marks=80
SECTION - I
2. Write short answers to any EIGHT (8) questions: (16)
- Show that f (x) = x2/3 + 6 is even function.
- Find the domain and range of f-1(x) where f (x) = 2
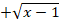
- Evaluate
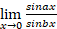
- Find
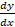 when y = (x - 5)(3 - x)dx
when y = (x - 5)(3 - x)dx
- Compute
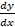 when y =
when y = 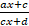
- Differentiate sec-1 x w.r.t. x
- If y = tan (p tan-l x)find

- Find f’ (x) when f (x) = x3e1/x
- Find
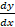 when y = a cos (
when y = a cos ( nx) + b sin (
nx) + b sin (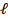 nx)
nx)
- Using Maclaurin's series expansion, write first two terms of f (x) =
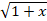
- Find
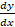 when y = sin-1
when y = sin-1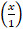
- Find critical values of f(x) = sin x + cos x
3. Write short answers to any EIGHT (8) questions : (16)
- Using differential, find
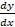 when xy -
when xy -  nx =
nx =
- Evaluate
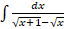
- Evaluate

- Find
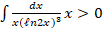
- Evaluate
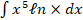
- Evaluate
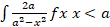
- Evaluate
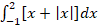
- Evaluate
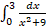
- Find the area bounded by y = cos x from x = -
 to x=
to x=
- Solve the differential equation x2(2y + 1)
 -1=0
-1=0
- Graph the solution region of 2x + 1
 0
0
- What are problem constraints?
4. Write short answers to any NINE (9) questions : (18)
- Find the point P on the join of A (1, 4) and B (5, 6) that is twice as far from A as B is from A and lies on the same side of A as B does.
- Two lines
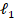 and
and  with respective slopes ml and m2 are parallel if m1 = m2
with respective slopes ml and m2 are parallel if m1 = m2
- If length of perpendicular from origin to a line is 5 units and its inclination is 120°, find slope and y-intercept of the line?
- Find the lines represented by x2-xy - 6y2 = 0, also find the angle between them.
- Find an equation of the line through (5, -8) and perpendicular to the join of A (-15, -8), B (10, 7)
- Find the coordinates of the points of intersection of the line 2x + y = 5 and x2 + y2 + 2x - 9 = 0
- Find an equation of a circle of radius 'a' and lying in the second quadrant such that it is tangent to both the axes.
- Find the focus and vertex of parabola y2 = - 8 (x - 3)
- Find equation of hyperbola with foci (±5, 0) and vertex (3, 0)
- Calculate projection of
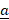 along
along 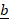 when
when 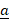 =
= 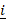 +
+ 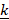 ,
, 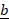 = j +
= j +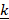
- Find the angle between the vectors
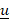 = 2
= 2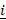 -
- 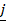 +
+ 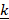 and
and 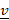 =-
=-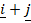
- Find the area of the triangle with vertices A (1, -1, 1) B (2, 1, -;1) C (-1, 1, 2)
- Find the direction cosines for
 , where P (2, 1, 5), Q (1, 3, 1)
, where P (2, 1, 5), Q (1, 3, 1)
SECTION-II
Note: Attempt any THREE questions.
5. (a) Find the values m and n, so that given function f(x) is continuous f (x)=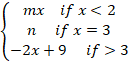
(b) Differentiate cos 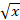 from the first principles.
from the first principles.
6. (a) Show that 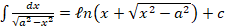
(b) Find equations of two parallel lines perpendicular to 2x - y' + 3 = 0 such that the product of the x – intercept and y - intercept of each is 3
7. (a) Evaluate 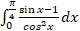
(b) Graph the feasible region and also find the corner points : 2x - 3y 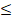 6, 2x + 3y
6, 2x + 3y 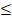 12,x
12,x 0 , y
0 , y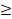 0
0
8. (a) Show that 2x + 3y - 13 = 0 is tangent to circle x2 + y2 +6x - 4y = 0
(b) Using vector prove that b = c cos A + a cos C
9. (a) Find an equation of the parabola whose focus is F (-3,4), and directrix line is 3x - 4y + 5 = 0
(b) Find the volume of the tetrahedron with the vertices A(0, 1, 2), B (3, 2, 1), C (1,2,1), D (5,5,6)
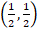

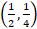
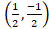
1
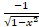

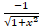
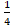
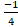
dx is equal to :
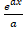
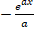
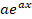
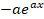
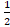

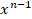
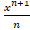
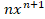
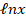

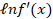


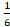
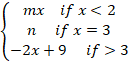
![]() from the first principles.
from the first principles. ![]()
![]()
![]() 6, 2x + 3y
6, 2x + 3y ![]() 12,x
12,x![]() 0 , y
0 , y![]() 0
0