Inter (Part-II) Multan Board 2015
Mathematics
Part II (Objective Type)
Time Allowed: 30 Minutes
Max. Marks: 20
Note: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.
Question #1
Circle the correct option i.e. A/B/C/D. Each part carries one mark.
(A) y = cos x
(B) y = sec x
(C) y = cosec2 x
(D) y = tan x
(A) 2
(B) 0
(C) 4
(D) -2
(A)
(B)
(C)
(D)
(A) 1
(B) 2
(C)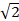
(D) 0
(A)
+
= c
(B)+
= 1
(C)+
= c
(D)-
= 0
(A) x + 2y =6
(B) x - 2y= 6
(C) x + 2y = -6
(D) x – 2y = -6
(A) (5,6)
(B) (-6,5)
(C)(5, 6)
(D) (6, -5 )
(A) Focii
(B) Vertices
(C) Covertices
(D) Directrix
(A) 2i – j
(B)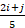
(C)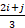
(D)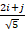
(A) 5
(B) 4
(C) -4
(D) 2
(A)
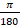
(B)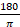
(C) 180π
(D)1
(A) 0
(B) -1
(C) 2
(D) 1
(A)
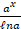
(B)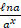
(C) axℓna
(D) ax
(A) 16
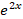
(B) 8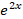
(C) 2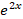
(D)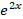
(A) –cos h x
(B) cos h x
(C) tan h x
(D) sec h x
(A) cosec2x
(B) tan2x
(C) sec2 x
(D) sec x
(A) ƒn(c) > 0
(B) ƒn(c) = 0
(C) ƒn(c) < 0
(D) ƒn(c)0
(A) x
(B) ℓnx
(C)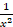
(D)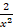
(A) sec x tan x
(B) ℓn(sex x tan x)
(C) ℓn(secx + tan x)
(D) ℓn(secx – tan x )
(A) ℓnx
(B) x
(C) ℓn(ℓnx)
(D)
Inter (Part-II) Multan Board 2015
Mathematics
Part II (Subjective)
Time Allowed: 2.30 Hours
Max. Marks: 80
Section I
2. Attempt any eight parts 8×2=16
3. Attempt any eight parts. 8×2=16
4. Attempt any nine parts. 9×2=18
SECTION-11
Note: Attempt any three questions.
Question #5
(a) Derive the formula ![]() = 1
= 1
(b) If y = (cos-1 x)2 prove that (1 – x2)![]() - xy1 -2 = 0
- xy1 -2 = 0
Question #6
(a) Evalute![]() dx
dx
(b) Find the area of the triangle region whose vertices are A(-5, 3), B(-2, 2), C(4, 2).
Question #7
(a) Solve the differential equation 2![]() tan y dx + (1 + ex) sec2 y dx = 0
tan y dx + (1 + ex) sec2 y dx = 0
(b) Maximize f(x, y) = x + 3y subject to constraints 2x + 5y ![]() 30, 5x + 4y
30, 5x + 4y ![]() 20, x
20, x ![]() 0, y
0, y![]() 0
0
Question #8
(a) The tangent to a ciecle at any point of the circle is perpendicular to the radial segment at point.
(b) Show that mid point of hypotenuse in a right triangle is equidistant from its vertices.
Question #9
(a) Find focus, vertex and directrix of the parabola (x + 1)2 = 8(y + 2)
(b) Prove that sin(a – β) = sin a cos β – cos a sin β