Inter (Part-II) MultanBoard 2015
Statistics
Part II (Objective Type)
Time Allowed: 20 Minutes 
Max. Marks: 17

Note: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.

Question #1
Circle the correct option i.e. A/B/C/D. Each part carries one mark.

• The value of Chi square may be:-

(A) Zero
(B) Positive
(C) Negative
(D) A and B but not C

• The components of time series are:-

(A) Four
(B) Three
(C) Two
(D) One

• A second degree parabola has:-

(A) Two constants
(B) Three constants
(C) 2 or 3 constant
(D) Less than 2 constants

• 01 Byte =

(A) 4 Bits
(B) 6 Bits
(C) 8 Bits
(D) 10 Bits

• In a Normal Distribution ß₂ is equal to:-

(A) 3α⁴
(B) 3
(C) α⁴/2
(D) 3α⁴/4

• The coefficient of skewness of Normal Distribution is:-

(A) Zero
(B) Positive
(C) Negative
(D) Both position and negative

• In normal curve the ordinate is highest at

(A) Mean
(B) Median
(C) Mode
(D) All of these

• If α²=5 and n = 2 then α² /x. is:-

(A) 2
(B) 2.5
(C) 3
(D) 5

• The possible samples in sampling without replacement is:- 

(A) N-n
(B) N+n
(C) C^N_n
(D) (N)ⁿ

• A value calculated from population is called a:-

(A) Statistic
(B) Mean
(C) Parameter
(D) Proportion

• For unbiasedness:-

(A) E(ẍ)≠µ
(B) E(ẍ)+ µ
(C) E(ẍ)= µ
(D) E(ẍ)- µ

• The hypothesis which is to be tested for possible rejection is:- 

(A) Simple
(B) Composite
(C) Null
(D) Alternative

• Two-tailed Test is used if:-

(A) H¹:µ<µ_o
(B) H₁:µ<µ_o
(C) H₁:µ#µ_o
(D) None of these

• In regression Σy is equal to:=

(A) 0
(B) Σy
(C) a
(D) hX

• If y=2+0.6x then the slope of the line is:-

(A) 2
(B) 2.6
(C) 0.6
(D) Zero

• If Σd²=0 then rank correlation is equal to:-

(A) 1
(B) Zero
(C) -1
(D) -1 and +1

• For a contingency table of order rxc the number of degree of freedom is equal to:-

(A) rc
(B) (r-1) (c)
(C) (c-1) (r)
(D) (r-1)(c-1)

Inter (Part-II) Multan Board 2015
Statistics
Part II(Subjective)
Time Allowed: 2.10 Hours 
Max. Marks: 83 

Section I

Q.2. Attempt any eight parts.

• What do you understand by Standard Normal Dist?
• In Normal Dist, mean is 100 and SD is 10, Find M.D and Q.D.
• Find Prob. that the value of standard normal variable is less than 2.
• In Normal dist, find
• (a) E|X-µ|
• (b) E|X-µ|2
• Define points of inflection in Normal  Dist
• Discuss estimation and its types
• What do you mean by Unbiased Estimator?
• Find point estimation of pop, Mean (µ) and standard error of mean
• Explain type-I and type-II error
• Define One-tailed and Two-tailed tests.
• How many are types of Computer?
• What are output devices of Computer?

Q.3. Attempt any eight parts.                                                              8x2=16

• What is Population?
• Write down any two advantages of sampling.
• What is non sampling error?
• What is random sampling?
• Define Stratum.
• What are the limitations of sampling?
• Define Simple Regression
• What is Principle of Least Squares?
• Define Dependent Variable.
• Define the term Correlation.
• What is meant by Negative Correlation?
• What is the range of Correlation Co-efficient?
  

Q.4. Attempt any six parts.                                          6x2=12

• Define +ve and -ve attributes.
• Define Contingency table.
• Define the term 'rank correlation co-efficient'.
• Define time series and give some examples.
• What are the names of basic components of time series?
• Give name of different methods of measuring the secular trend?
• What is meant by Seasonal Variation'?
• Write the equation of 2nd degree parabola.
• Differentiate between Signal and Noise.

SECTION-II

NOTE: - Attempt any three questions.

Question #5
(a) In a normal distribution µ =113.49 and Q1=100, find value of ß2
(b) If X~N(10; 4 ) then find   (i) P( X>16 )   (ii) P(8< x<12 )

Question #6
(a) Given the population values 2, 5, 8. Taking all possible sample of size 2 with replacement form the sampling distribution of ẍ. Compute µ ẍ and α2/x and verify that (i) µ ẍ = µ (ii) α2/x= α/n
(b) If Mean and Variance of a population are 5 and 2.15, what would be the standard error if sample of size 4 are drawn with replacement?

Question #7
(a) A random sample of size 36 is taken from a normal population with known variance α2=25 If  x=42.6, find 95% confidence interval for the population mean (µ).
(b) Given the following information:- n=30, x=15.2, α=3, Test the hypothesis that µ=15.8 at α=0.05.

Question #8
(a) Compute 'r' from the following data:-    X = 14.6, Y =12.7, Σ(x-x)2=115.96    Σ(y-y)2=59.04, Σ (x-x)(y-y)=5395,    n =10
(b) Construct the regression equation of demand on price, in the form Y=a+bx.         

Question #9
(a) 750 students appeared in an examination and 470 were successful. 465 had attended classes and 58 of them failed. Calculate the coefficient of association to discuss association between attending classes and success.
(b) Why the method of least squares derive a linear trend to the following results for the years 1985 to 1994 (both inclusive):- Σx .0, ΣY = 322 , ΣXY =1550, Σx2.330. Find out trend values as well.

SECTION-Ill (PRACTICAL)

Question #10. NOTE: Attempt any three parts.                                                    3x5=15

(a) A population consists of 2, 4, 6, 8.Find
(i) Mean, variance and standard deviation of population
(ii) Make sample of size 3 without replacement and find means of all the samples.
(iii) Make sampling dist - of ẍ
(iv) Verify the result µx=µ, S.E(ẍ)=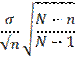

(b) Given that X1= 75, n1=9, )= 1482
X₂ = 60, n₂ =16 ∑(x₂- X₂) =1830 and assuming that two samples were randomly selected from the Normal Population 
in which α21= α2 (but unknown). Calculate an 80 % confidence interval for the difference between two population means.

(c) Calculate the correlation coefficient between the variable X and y represented in the 
following table:-

(d) A random sample of 15 men and 15 women were polled as to their desires concerning
the ownership of television set. The following data are resulted:-

 Test the hypothesis that desire to own a television set is independent of sex at .05 level of significance.

(e) From the data given below:-

Obtain trend values using method of Semi-Average.